
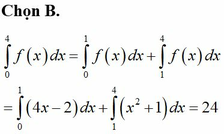
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

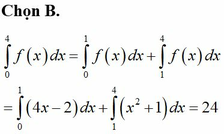

Vì 0<a<b<c<d<e<f nên :
(a-b) < 0 ; (c-d) < 0 ; (e-f) < 0
và (b-a) > 0 ; (d-c) > 0 ; (f-e) > 0
Do đó (a-b)(c-d)(e-f) < 0 ; (b-a)(d-c)(f-e) > 0
Mà (a-b)(c-d)(e-f).x=(b-a)(d-c)(f-e) <=> x = -1

Ta có:
\(f\left(x\right)=0\), do đó với mọi giá trị của x thì đa thức này bằng 0
Ta có:
\(f\left(1\right)=a.1^2+b.1+c=a+b+c=0\)
\(\Rightarrow a+b+c+3=0+3=3\)
Vậy \(a+b+c=3\)

Xét tử \(\left|4-x\right|+\left|x+2\right|\ge0\)
Xét mẫu \(\left|x+5\right|+\left|x-3\right|\ge0\)
Do đó \(\frac{\left|4-x\right|+\left|x+2\right|}{\left|x+5\right|+\left|x-3\right|}\ge0\)
Nhưng đề bài cho \(\frac{\left|4-x\right|+\left|x+2\right|}{\left|x+5\right|+\left|x-3\right|}=-\frac{1}{2}<0\) nên không có giá trị nào của x thỏa mãn.

3(x-2)-4(2x+1)-5(2x+3)=50
<=>(3x-6)-(8x+4)-(10x+15)=50
<=>3x-6-8x-4-10x-15=50
<=>(3x-8x-10x)+(-6-4-15)=50
<=>-15x-25=50
<=>-15x=75
<=>x=-5
\(3\frac{1}{2}:\left(4-\frac{1}{3}\left|2x+1\right|\right)=\frac{21}{22}\)
<=>\(4-\frac{1}{3}\left|2x+1\right|=\frac{7}{2}:\frac{21}{22}=\frac{11}{3}\)
<=>\(\frac{1}{3}\left|2x+1\right|=4-\frac{11}{3}=\frac{1}{3}\)
<=>\(\left|2x+1\right|=1\)
<=>2x+1=1 hoặc 2x+1=-1
<=>2x=0 hoặc 2x=-2
<=>x=0 hoặc x=-2
Vậy......................