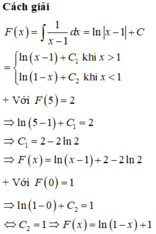Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Ta có:
\(f\left(1\right).f\left(-1\right)=\left(a+b\right).\left(-a+b\right)\)
\(\Rightarrow\left(a+b\right)\left(-a+b\right)=\left(a+b\right)^2\)
\(\Rightarrow-a+b=a+b\)
\(\Rightarrow a=-a\)
\(a\ne0\) thì làm sao có a thỏa mãn được?
Trần Thùy Dung ko biết thì đừng có làm. 5 - 3a - 3b = 5. Bài này trong violympic.

Từ \(f\left(x\right)+f\left(\frac{1}{x}\right)=x^2\); lần lượt thay \(x=2\) và \(x=\frac{1}{2}\) vào, ta có:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\) và \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\Leftrightarrow3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\)
Giải hệ phương trình với 2 ẩn \(f\left(2\right)\) và \(f\left(\frac{1}{2}\right)\)
Tìm được \(f\left(2\right)=\frac{-13}{32}\)
Ta có \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) (1)
Thay \(x\rightarrow\frac{1}{x}\) được \(f\left(\frac{1}{x}\right)+3f\left(x\right)=\frac{1}{x^2}\)
\(\Leftrightarrow3f\left(\frac{1}{x}\right)+9f\left(x\right)=\frac{3}{x^2}\) (2)
Lấy (2) trừ (1) theo vế : \(8f\left(x\right)=\frac{3}{x^2}-x^2\)
\(\Leftrightarrow f\left(x\right)=\frac{1}{8}\left(\frac{3}{x^2}-x^2\right)\)
Vậy f(2) = -13/32

a/ f(x) = 0 => x2 + 4x - 5 = 0 => (x - 1)(x + 5) = 0 => x = 1 hoặc x = -5
Vậy x = 1 , x = -5
b/ f(x) > 0 => x2 + 4x - 5 > 0 => (x - 1)(x + 5) > 0 => x - 1 > 0 và x + 5 > 0 => x > 1 và x > -5 => x > 1
hoặc x - 1 < 0 và x + 5 < 0 => x < 1 và x < -5 => x < -5
Vậy x > 1 hoặc x < -5
c/ f(x) < 0 => x2 + 4x - 5 < 0 => (x - 1)(x + 5) < 0 => x - 1 > 0 và x + 5 < 0 => x > 1 và x < -5 => vô lí
hoặc x - 1 < 0 và x + 5 > 0 => x < 1 và x > -5 => -5 < x < 1
Vậy -5 < x < 1

Biến đổi :
\(4\sin x+3\cos x=A\left(\sin x+2\cos x\right)+B\left(\cos x-2\sin x\right)=\left(A-2B\right)\sin x+\left(2A+B\right)\cos x\)
Đồng nhất hệ số hai tử số, ta có :
\(\begin{cases}A-2B=4\\2A+B=3\end{cases}\)\(\Leftrightarrow\begin{cases}A=2\\B=-1\end{cases}\)
Khi đó \(f\left(x\right)=\frac{2\left(\left(\sin x+2\cos x\right)\right)-\left(\left(\sin x-2\cos x\right)\right)}{\left(\sin x+2\cos x\right)}=2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\)
Do đó,
\(F\left(x\right)=\int f\left(x\right)dx=\int\left(2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\right)dx=2\int dx-\int\frac{\left(\cos x-2\sin x\right)dx}{\sin x+2\cos x}=2x-\ln\left|\sin x+2\cos x\right|+C\)

Bài 2
a) 4^100 = (2^2)^100= 2^200
Mà 2^202 > 2^200 => 4^100 < 2^202
b)Ta có: 31^5 <32^5 = (2^5)^5 = 2^25 (1)
17^7 > 16^7= (2^4)^7= 2^28 (2)
Từ (1) và (2) => 31^5<17^7

Đa thứ f(x) có dạng : ax2+bx+c
Theo đề ta có: 25a+5b+c=25a-5b+c
<=>5b=-5b
=>b=0
Do đó f(x) phải có dạng ax2+c
Ta thấy ax2+c=a.(-x)2+c
=>f(x)=f(-x) với mọi x thuộc R

Ta biến đổi :
\(f\left(x\right)=\cos3x\cos5x=\frac{\cos5x+\cos2x}{2}=\frac{1}{2}\cos8x+\frac{1}{2}\cos2x\)
Khi đó :
\(I=\int f\left(x\right)dx=\frac{1}{2}\int\cos8xdx+\frac{1}{2}\int\cos2xdx=\frac{1}{16}\sin8x+\frac{1}{4}\sin2x+C\)

Chọn đáp án C
Phương pháp
Sử dụng công thức nguyên hàm:
![]()
dựa dữ kiện đề bài tìm được C, từ đó tính F(2)-F(-1)