LT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
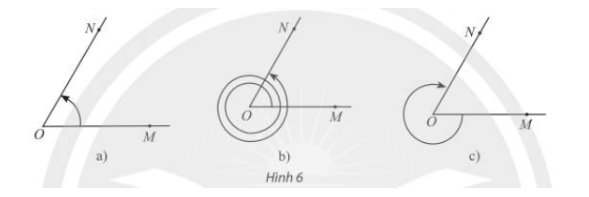
a, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o\)
b, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o+2\cdot360^o=780^o\)
c, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(\dfrac{5}{6}\cdot\left(-360^o\right)=-300^o\)
Công thức tổng quát của số đo góc lượng giác (OM, ON) \(=60^o+360^o\cdot k,k\in Z\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có:
\((O'u',O'v') = (Ou,Ov) + k2\pi \,\, = \, - \frac{{4\pi }}{3}\, + k2\pi \,\,\,\,\,\,\,\,(k \in \mathbb{Z})\)
CM
12 tháng 1 2017
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
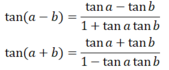
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
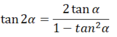
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
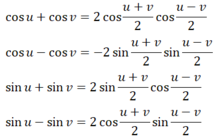
\(\begin{array}{l}\cos \left( {\alpha + \alpha } \right) = \cos 2\alpha = \cos \alpha \cos \alpha - \sin \alpha sin\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha \\ = {\cos ^2}\alpha + {\sin ^2}\alpha - 2{\sin ^2}\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}a - 1\end{array}\)
\(\tan 2\alpha = \tan \left( {\alpha + \alpha } \right) = \frac{{\tan \alpha + \tan \alpha }}{{1 - \tan \alpha .\tan \alpha }} = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\)
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
Ta có:
\(\begin{array}{l}\cos \alpha \cos \beta = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha + \cos \beta } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \sin \beta = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta - \cos \alpha } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \cos \beta = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha + \sin \beta } \right)\end{array}\)
NG
0
23 tháng 6 2016
bài này dễ thôi bạn
thay x= x+ k6pi vào hàm số y=f(x)= sin\(\frac{x}{3}\) ta dc
sin\(\frac{x+k6pi}{3}\) =sin\(\frac{x}{3}+k2pi\) ( vì k2pi "số chẵn lần của π" nên có thể bỏ được)
suy ra sin\(\frac{x}{3}\) =sin\(\frac{x}{3}\) =f(x) ( dpcm)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
k ở đây được hiểu là "một số nguyên bất kì", giống hay khác nhau đều được
Ví dụ:
\(sinx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Thì "k" trong \(\dfrac{\pi}{6}+k2\pi\) và "k" trong \(\dfrac{5\pi}{6}+k2\pi\) không liên quan gì đến nhau (nó chỉ là 1 kí hiệu, có thể k trên bằng 0, k dưới bằng 100 cũng được, không ảnh hưởng gì, cũng có thể 2 cái bằng nhau cũng được).
Khi người ta ghi 2 nghiệm đều là "k2pi" chủ yếu do... lười biếng (kiểu như mình). Trên thực tế, rất nhiều tài liệu cũ họ ghi các kí tự khác nhau, ví dụ 1 nghiệm là \(\dfrac{\pi}{6}+k2\pi\), 1 nghiệm là \(\dfrac{5\pi}{6}+n2\pi\) để tránh học sinh phát sinh hiểu nhầm đáng tiếc rằng "2 cái k phải giống hệt nhau về giá trị".
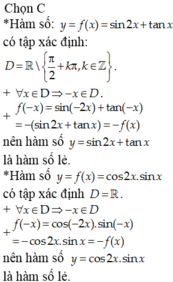
kinh đấy
tra google nha có thật là hc lớp 11 k