Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số trên có dạng y = ax + b => Hàm số đồng biến khi a > 0 , nghịch biến khi a<0
a) Hàm số nghịch biến khi \(m-2< 0\Rightarrow m< 2\)
b) Hàm số nghịch biến khi \(m+1< 0\Rightarrow m< -1\)

1.
Để hàm đồng biến trên R \(\Leftrightarrow m-2>0\Leftrightarrow m>2\)
\(\Rightarrow\) có \(2019-3+1=2017\) giá trị nguyên của m
2.
Câu 2 làm gì có m nào mà tìm bạn? Chắc bạn ghi sai hàm \(f\left(x\right)\)

Câu 1:
\(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-sin^2x=1-\left(\frac{4}{5}\right)^2=\frac{9}{15}\)
\(\Leftrightarrow cos^2x=\frac{\pm3}{5}\).
Câu 2:
Đường tròn \(\left(C\right)\)có tâm \(I\left(2,-1\right)\)bán kính \(R=\sqrt{25}=5\).
Gọi \(d\)là tiếp tuyến của đường tròn \(\left(C\right)\)tại điểm \(M\). Khi đó \(IM\)và \(d\)vuông góc với nhau.
\(\Rightarrow\overrightarrow{IM}=\left(3,4\right)\)là một vector pháp tuyến của \(d\)
Suy ra phương trình \(d:3\left(x-5\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-27=0\).

y' là đạo hàm bậc nhất của y. Bạn đọc sách toán phổ thông phần đạo hàm/ tìm max min của hàm số hoặc google search để tìm hiểu rõ hơn.

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4a=-28\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=-13\end{matrix}\right.\)
b: Vì (d)//y=-2/3x+1 nên a=-2/3
Vậy: (d): y=-2/3x+b
Thay x=4 và y=-3 vào (d), ta được:
b-8/3=-3
hay b=-1/3

1.A. Ta thấy để hàm số xác định thì x-m\(\ne\)0 hay x\(\ne\)m mà vì x\(\in\)(0,1) nên để x\(\ne\)m thì m\(\notin\)(0,1)=>m>=1 hoặc m<=0
2A để A giao B khác 0 thì 2m-1<=m+3 hay m<=4
3C.A giao B =A khi \(\left\{{}\begin{matrix}m< =-1\\m+5>=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< =1\\m>=-2\end{matrix}\right.\)

pt2 <=> 4x^2 -4x+1+4y^2 -4y+1=18
<=>x^2+y^2-3=x+y+1
thay vào pt 1 ta đk
căn (x+2) +3 căn ( y-1) =căn ( 5(x+y+1))
đặt căn (x+2)=a căn (y-1)=b
pt1 <=> a+3b=căn (5a^2+5b^2)
bình phương hai vế ta đk
a^2 +6ab+9b^2 =5a^2+5b^2
<=>4a^2-6ab-4b^2=0
<=>(2a+b)(a-2b)=0
sau đó bạn giải từng trường hợp rồi thay ngược lại pt 2 mà giải ra x với y
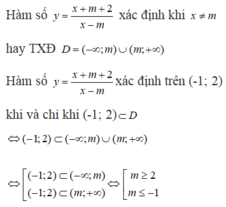

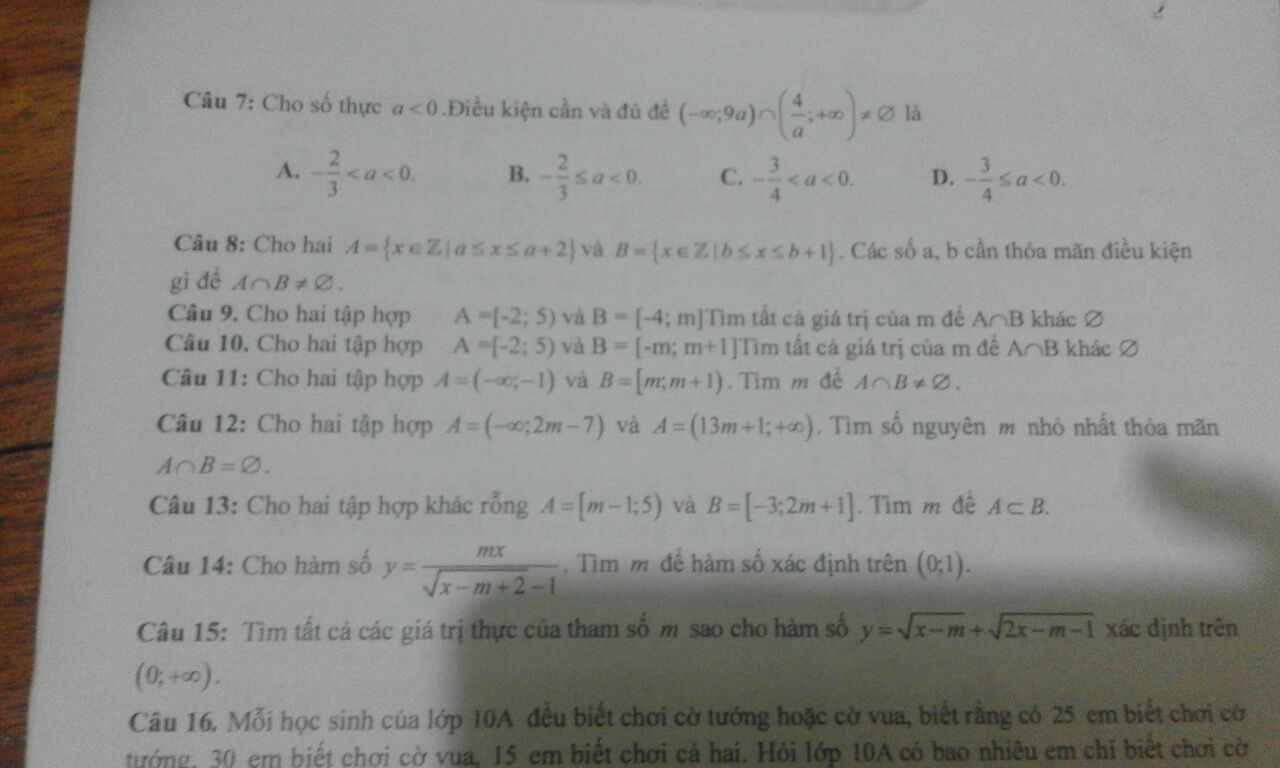 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!