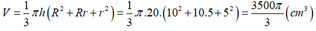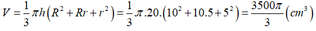Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1: Áp dụng công thức
- Với hình nón cụt có các bán kính các đáy là r1, r2, đường sinh l và chiều cao h thì :
Sxq= π(r1+ r2).l
V = 1/3πh(r12+ r22+ r1 r2)
Như vậy :
Diện tích xung quanh hình nón cụt thì bằng tích của số π với tổng hai bán kính và với đường sinh.
Thể tích của hình nón cụt thì bằng 1/3 tích của số π với đường cao h và tổng bình phương các bán kính cộng thêm tích của hai bán kính .
Cách 2: Vì hình nón cụt được cắt ra từ hình nón nên ta có thể tính
V(nón cụt )=V(nón lớn )-V(nón nhỏ )
S(xq nón cụt )=S(xq nón lớn )-S(xq nón nhỏ )

Cách 1: Áp dụng công thức
- Với hình nón cụt có các bán kính các đáy là r 1 , r 2 , đường sinh l và chiều cao h thì :
S X q = π r 1 + r 2 ⋅ 1 V = 1 / 3 π h r 1 2 + r 2 2 + r 1 r 2
Như vậy :
Diện tích xung quanh hình nón cụt thì bằng tích của số π với tổng hai bán kính và với đường sinh.
Thể tích của hình nón cụt thì bằng 1/3 tích của số π với đường cao h và tổng bình phương các bán kính cộng thêm tích của hai bán kính .
Cách 2: Vì hình nón cụt được cắt ra từ hình nón nên ta có thể tính
V(nón cụt )=V(nón lớn )-V(nón nhỏ )
S(xq nón cụt )=S(xq nón lớn )-S(xq nón nhỏ )

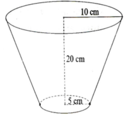
a, Dung tích của xô là: V = 1 3 πh r 1 2 + r 1 r 2 + r 2 2
với r 1 = 5cm, r 2 = 10cm; h = 20cm
Thay số liệu và tính toán ta được V = 3663 c m 3
b, Tính được đường sinh của xô dạng hình nón cụt là l = 20,6cm
Diện tích tôn để làm xô mà không kể diện tích các chỗ ghép là S = S x q + S 1 = π r 1 + r 2 l + πr 1 2 với S 1 là diện tích đáy nhỏ của đáy dưới của xô
Thay số vào và tính toán ta được S = 1048,76 c m 2

Lời giải:
Diện tích xung quanh hình nón:
$\pi (r+R).l=\pi (6+3).4=36\pi$ (cm vuông)
Diện tích toàn phần:
$36\pi+\pi r^2+\pi R^2=36\pi +\pi.3^2+\pi. 6^2=81\pi$ (cm vuông)
Thể tích:
Chiều cao hình nón: $\sqrt{4^2-(6-3)^2}=\sqrt{7}$ (cm)
$\frac{1}{3}\pi (r^2+R^2+r.R)h=\frac{1}{3}\pi (3^2+6^2+3.6).\sqrt{7}=21\sqrt{7}\pi$ (cm khối)