Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


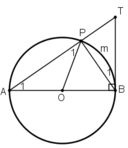
là góc tạo bởi tiếp tuyến BT và dây cung BP.
=
sđ
![]() (1)
(1)
là góc nội tiếp chắn cung
![]()
=
sđ
![]() (2)
(2)
Lại có =
(∆OAP cân) (3)
Từ (1), (2), (3), suy ra =


Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

(Quá lực!!!)
E N A B C D O H L
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)

B 1 ^ l à g ó c t ạ o b ở i t i ế p t u y ế n B T v à d â y B P
⇒ B 1 ^ = 1 2 . s đ P B ⏜
Xét tam giác APO có OA=OP=R
⇒ ∆ A P O c â n t ạ i O ⇒ A 1 ^ = P B T ^ (1)
Xét tam giác APO cân tại O ⇒ A 1 ^ = P 1 ^ (2)
Từ (1) và (2) suy ra B 1 ^ = P 1 ^ h a y A P O ^ = P B T ^