Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:OI=OA-IA=R-r
nen (O) tiếp xúc (I) tại A
b: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
Xét (I) có
ΔADO nội tiếp
AO là đường kính
Do đó: ΔADO vuông tại D
=>OD//CB
Xét ΔACBcó DO//CB
nên AD/AC=AO/AB=1/2
=>D là trung điểm của AC
Xét ΔAOC có AI/AO=AD/AC
nên ID//OC và ID=OC/2

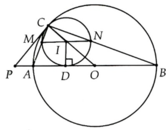
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm

a) Tam giác ABC nội tiếp đường tròn (O) đường kính BC
=> OA=OB=OC và O là trung điểm của BC
=> Tam giác ABC vuông tại A
=> góc BAC = 90 độ
b) DO tam giác HAK nội tiếp đường tròn (I)
Lại có góc HAK = 90 độ
=> HK là đường kính của (I)
=> HK đi qua I
=> H,I,K thẳng hàng
c) Đề bài ghi ko rõ
d) 3 điểm nào?

Cái này chắc chỉ là suy luận thooi vậy giả thuyết đầu bài cho thừa
Vì A thuộc (I) mà A cũng thuộc (O) (AB là đường kính ) => (I) và (O) tiếp xúc nhau tại A

A C E D M I O' B O
Vì em là học sinh lớp 9 nên cô chỉ hưỡng dẫn thôi nhé :) Cố gắng thi tốt nhé :)
a. ADBE là hình thoi vì có hai đường chéo vuông góc và cắt nhay tại trung điểm mỗi đường.
b. Tứ giác DMBI có góc DMB + góc DIB = 180 độ nên nó là tứ giác nội tiếp.
c. Cô nghĩa là chứng minh B, I, E thẳng hàng ms đúng, em xem lại xem.
Ta có: \(\widehat{MIE}=\widehat{MDB}=\widehat{MEB}\) suy ra tam gaisc MIE cân tại M hay MI = ME. Lại có ME = MD nên MD = MI.
d.Hệ thức có được là do \(\Delta BDC\sim\Delta IMC\left(g-g\right)\)
e. Ta chứng minh \(\widehat{O'IC}=\widehat{MIB}\)
Thật vậy, \(\widehat{O'IC}=\widehat{O'CI}=\widehat{DEA}=\widehat{MDO}=\widehat{MIB}\).
Khi đó \(90^0=\widehat{O'IC}+\widehat{O'IB}=\widehat{MIB}+\widehat{O'IB}\)
Vậy MI vuông góc O'I hay MI là tiếp tuyến (O')
