Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 7:
a: Xét ΔOAM vuông tại A có
\(\cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AOM}=60^0\)
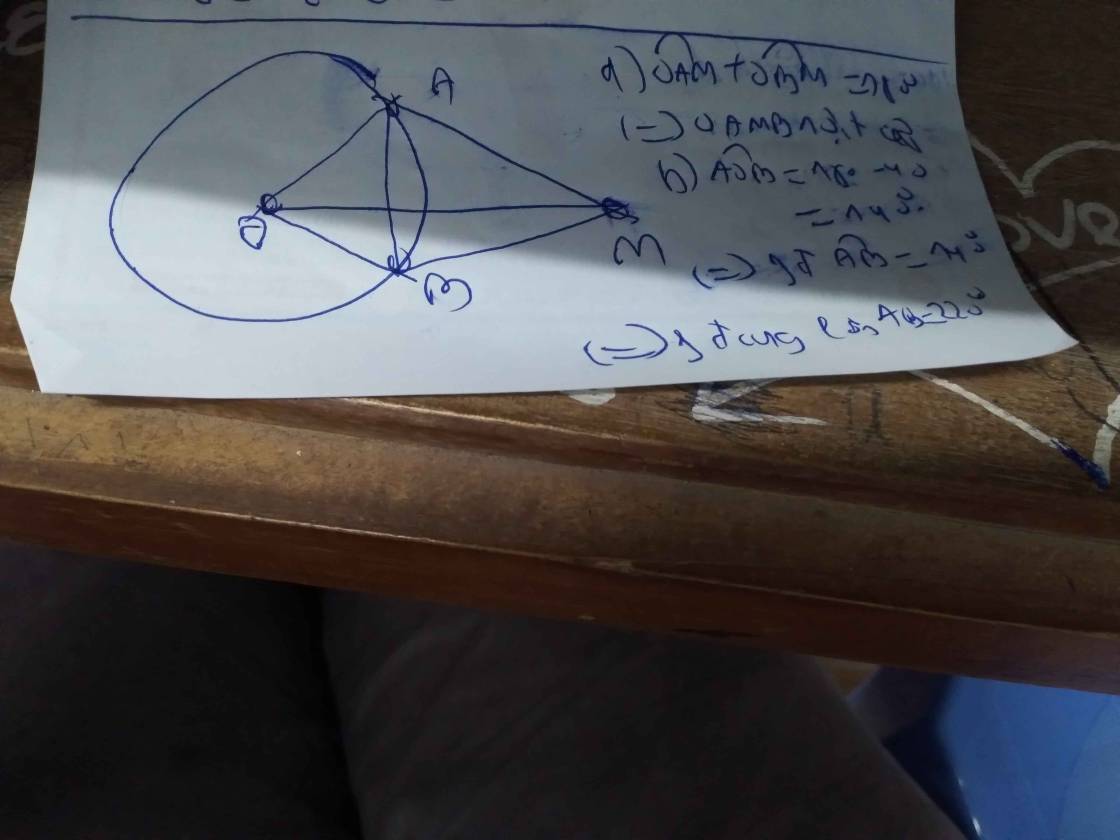
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=180^0\)
Do đó: OAMB là tứ giác nội tiếp
Suy ra: \(\widehat{AOB}=180^0-36^0=144^0\)

a: ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}=90^0\)
b: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>AB\(\perp\)BD
Ta có: AB\(\perp\)BD
AB\(\perp\)OC
Do đó: BD//OC

2:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: ΔONP cân tại O
mà OK là trung tuyến
nên OK vuông góc NP
góc OKM=góc OAM=góc OBM=90 độ
=>O,P,A,M,B cùng nằm trên đường tròn đường kính OM
góc AKM=góc AOM
góc BKM=góc BOM
mà góc AOM=góc BOM
nên góc AKM=góc BKM
=>KM là phân giác của góc AKB
Xét ΔODB có OD=OB(gt)
nên ΔODB cân tại O(Định nghĩa tam giác cân)
Xét ΔOBD cân tại O có \(\widehat{DOB}=60^0\left(sđ\stackrel\frown{BD}=60^0\right)\)
nên ΔOBD đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{OBD}=60^0\)(Số đo của một góc trong ΔOBD đều)
\(\Leftrightarrow\widehat{ABM}=60^0\)
Ta có: ΔBAM vuông tại A(gt)
nên \(\widehat{ABM}+\widehat{AMB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{AMB}+60^0=90^0\)
hay \(\widehat{AMB}=30^0\)
Vậy: \(\widehat{AMB}=30^0\)