Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác CDOE có \(\widehat{CDO}+\widehat{CEO}=180^0\)
nên CDOE là tứ giác nội tiếp
b:
Xét (O) có
CD là tiếp tuyến
CE là tiếp tuyến
Do đó: CD=CE và CO là phân giác của góc DCE
Ta có: ΔODC vuông tại D
mà DB là đường trung tuyến
nên DB=OB=BC
Xét ΔOBD có OB=OD=DB
nên ΔOBD đều
=>\(\widehat{DOB}=60^0\)
\(\Leftrightarrow\widehat{DCO}=30^0\)
=>\(\widehat{DCE}=60^0\)(Do CO là phân giác của góc DCE)
Xét ΔDCE có CD=CE
nên ΔCDE cân tại C
mà \(\widehat{DCE}=60^0\)
nên ΔCDE đều

Lời giải 1 bài toán tương tự - Dài và khó
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube

a ) Xét tứ giác CDOE ta có :
\(\left\{{}\begin{matrix}\widehat{CDO}=90^0\\\widehat{CEO}=90^0\end{matrix}\right.\) ( Tiếp tuyến vuông góc với bán kính )
\(\Rightarrow\widehat{CDO}+\widehat{CEO}=180^0\)
\(\Rightarrow CDOE\) là tứ giác nội tiếp ( đpcm )
b ) Ta có : \(OC=2R=12cm\)
Theo tỉ số lượng giác cho tam giác COD :
\(\widehat{DCO}=\sin^{-1}\left(\frac{OD}{OC}\right)=\sin^{-1}\left(\frac{6}{12}\right)=30^0\)
\(\Rightarrow\widehat{DCE}=2\widehat{DCO}=2.30^0=60^0\)
Mà tam giác DCE cân tại C do \(CD=CE\)
Tam giác cân có góc ở đỉnh bằng 60 độ nên DCE là tam giác đều .
c ) Xét \(\Delta CDM\) và \(\Delta CND\) ta có :
\(\left\{{}\begin{matrix}\widehat{DCM}:chung\\\widehat{MDC}=\widehat{DNC}\left(=\frac{1}{2}sđ\stackrel\frown{MD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta CDM\sim\Delta CND\left(g-g\right)\)
\(\Rightarrow\frac{CD}{CN}=\frac{CM}{CD}\)
\(\Rightarrow CD^2=CM.CN\left(đpcm\right)\)
OC sao = 12 được ạ.
Vì đường kính nó là 6 mà chứ đâu phải bán kính là 6 đâu

a, Vì CA = CM ( tc tiếp tuyến cắt nhau )
OA = OM = R
=> OC là đường trung trực đoạn AM
=> OC vuông AM
^AMB = 900 ( góc nội tiếp chắn nửa đường tròn )
=> AM vuông MB (1)
Ta có : DM = DB ( tc tiếp tuyến cắt nhau )
OM = OB = R
=> OD là đường trung trực đoạn MB
=> OD vuông MB (2)
Từ (1) ; (2) => OD // AM
b, OD giao MB = {T}
OC giao AM = {U}
Xét tứ giác OUMT có ^OUM = ^UMT = ^MTO = 900
=> tứ giác OUMT là hcn => ^UOT = 900
Vì CD là tiếp tuyến (O) với M là tiếp điểm => ^OMD = 900
Mặt khác : BD = DM ( tc tiếp tuyến cắt nhau )
CM = AC ( tc tiếp tuyến cắt nhau )
Xét tam giác COD vuông tại O, đường cao OM
Ta có : \(OM^2=CM.MD\)hay \(OM^2=AC.BD\)=> R^2 = AC.BD
c, Gọi I là trung điểm CD
O là trung điểm AB
khi đó OI là đường trung bình hình thang BDAC
=> OI // AC mà AC vuông AB ( tc tiếp tuyến ) => OI vuông AB
Xét tam giác COD vuông tại O, I là trung điểm => OI = IC = ID = R
Vậy AB là tiếp tuyến đường tròn (I;CD/2)

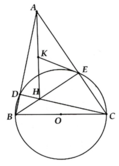
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm