Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B O C 2R R
TA CÓ AB\(=2R\)
\(\Leftrightarrow0B=BC=R\)
HAY \(BC=\frac{1}{2}AB\)
CÓ NGHĨA BC LÀ NỮA TRUNG ĐIỂM CỦA BC
\(\Rightarrow AC\perp BC\)ĐỊNH LÝ 3
CHO \(R=2cm\)tính cho nó rễ
áp dụng địn lý pi ta gao trong tam giác ABC vuông tại C
\(\Rightarrow AB^2=AC^2+BC^2\)
\(\Rightarrow AC^2=16-4\)
\(\Rightarrow AC=\sqrt{12}cm\)
vậy .............

a) Ta có:
OB = OC = R (vì B, C nằm trên (O ; R))
DB = DC = R ( vì B, C nằm trên (D ; R))
Suy ra : OB = OC = DB = DC.
Vậy tứ giác OBDC là hình thoi.
b) Ta có: OB = OD = BD = R
∆OBD đều ⇒ˆOBD=60∘
Vì OBDC là hình thoi nên:
ˆCBD=ˆOBC=12ˆOBD=30∘CBD^=OBC^=12OBD^=30∘
Tam giác ABD nội tiếp trong (O) có AD là đường kính nên:
ˆABD=90∘ABD^=90∘
Mà ˆOBD+ˆOBA=90∘OBD^+OBA^=90∘
Nên ˆOBA=ˆABD–ˆOBD=90∘–60∘=30∘OBA^=ABD^–OBD^=90∘–60∘=30∘
c) Tứ giác OBDC là hình thoi nên OD ⊥ BC hay AD ⊥ BC
Ta có: AB = AC ( tính chất đường trung trực)
Suy ra tam giác ABC cân tại A (1)
Mà ˆABC=ˆOBC–ˆOBA=30∘+30∘=60∘ABC^=OBC^–OBA^=30∘+30∘=60∘. (2)
Từ (1) và (2) suy ra tam giác ABC đều.
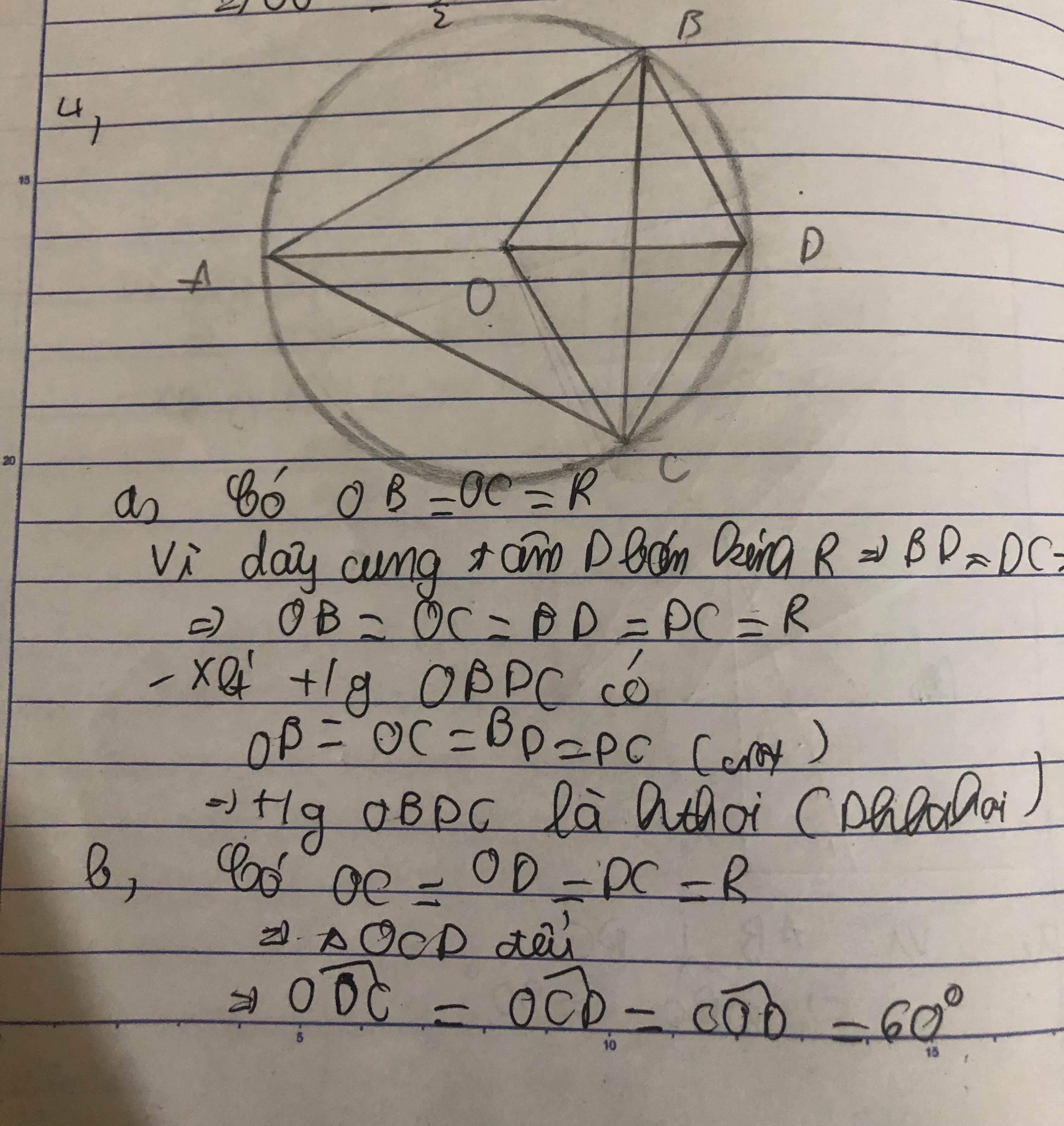
$AB$ là đường kính $(O)$
$\Rightarrow OB=\dfrac{AB}{2}=\dfrac{2R}{2}=R$
Vì $C\in(O)$
$\Rightarrow OC=R$
Xét $\Delta OBC$:
$OC=OB=BC=R$
$\Rightarrow \Delta OBC$ đều
$\Rightarrow \widehat{OBC}=60^o$ hay $\widehat{ABC}=60^o$
Vậy $\widehat{ABC}=60^o$