Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
AB,CD là dây
AB=CD
OI là khoảng cách từ O đến AB
OK là khoảng cách từ O đến CD
Do đó: OI=OK
c: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
=>góc BAD+góc ABC=180 độ
mà góc BAD+góc BCD=180 độ(ABCD là tứ giác nội tiếp)
nên góc ABC=góc BCD=180/2=90 độ
=>ABCD là hình chữ nhật

a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)

Tam giác ABC có 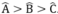 nên suy ra :
nên suy ra :
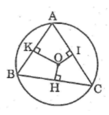
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC > AC > AB nên suy ra:
OH < OI < OK (dây lớn hơn gần tâm hơn)

Xét ΔABC có \(\widehat{BAC}>\widehat{ABC}>\widehat{ACB}\)
mà BC là cạnh đối diện của góc BAC
và AC là cạnh đối diện của góc ABC
và AB là cạnh đối diện của góc ACB
nên BC>AC>AB
Xét (O) có
BC,AC,AB là các dây
BC>AC>AB
OH,OI,OK lần lượt là khoảng cách từ tâm O đến các dây BC,AC,AB
Do đó: OH<OI<OK


a: Vì I là trung điểm của AB
và AB=2R
nên I trùng với O
=>OI=0
Ta có: ΔOCD cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)CD tại K
Ta có: K là trung điểm của CD
=>\(KC=KD=\dfrac{CD}{2}=\dfrac{R\sqrt{3}}{2}\)
Ta có: ΔOKC vuông tại K
=>\(OK^2+KC^2=OC^2\)
=>\(OK^2+\left(\dfrac{R\sqrt{3}}{2}\right)^2=R^2\)
=>\(OK^2=R^2-\left(\dfrac{R\sqrt{3}}{2}\right)^2=R^2-\dfrac{3R^2}{4}=\dfrac{1}{4}\cdot R^2\)
=>OK=1/2R
b:C1: Ta có: OI=0
OK=1/2R
=>OI<OK
C2: Xét (O) có
AB là đường kính
CD là dây
=>CD<AB
Xét (O) có
CD,AB là các dây của (O)
AB>CD
OI,OK lần lượt là khoảng cách từ O xuống AB,CD
Do đó: OI<OK