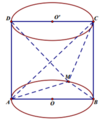
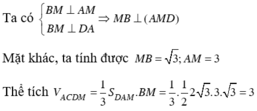Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi (C) là đường tròn tâm O bán kính r, \(\left(C_1\right)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng qua tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \(\left(C_1\right)\).
Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') và \(\left(C_1\right)\).


Do tứ giác ABMM' là hình bình hành nên \(\overrightarrow{BA}=\overrightarrow{MM'}\). Từ đó suy ra M' là ảnh của M qua phép tịnh tiến theo vectơ \(\overrightarrow{BA}\). Từ đó suy ra tập hợp các điểm M' là đường tròn (C'), ảnh của (C) qua phép tịnh tiến theo vectơ \(\overrightarrow{BA}\)

Do tứ giác ABMM’ là hình bình hành nên B A → = M M ' → là. Từ đó suy ra M' là ảnh của M qua phép tịnh tiến theo vectơ B A → .Từ đó suy ra tập hợp các điểm M' là đường tròn (C') , ảnh của C qua phép tịnh tiến theo vectơ BA→.

Đáp án B.
Kẻ ![]()
Vẽ O'H ⊥ A'B thì H là trung điểm của A'B.
∆ O'A'H vuông tại H nên
![]()
![]()
![]()
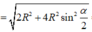
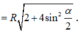

Lấy A' đối xứng với A qua d. Khi đó: AM+MB=A'M+MB>=A'B.
Vậy (AM+MB)min <=> A', M, B thẳng hàng.
Cách dựng: Lấy A' đối xứng A qua d, A'B cắt d tại M. M là điểm cần tìm