Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

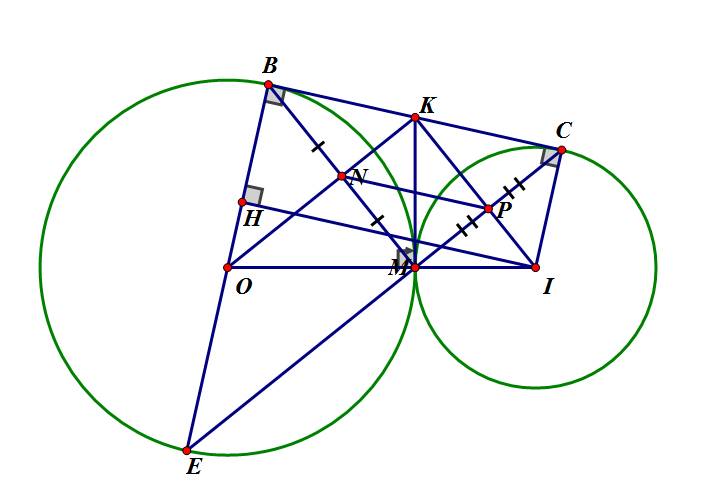
a) Trong (O) có: KB,KM là hai tiếp tuyến cắt nhau tại K.
\(\Rightarrow KB=KM\left(1\right)\).
Trong (I) có: KC,KM là hai tiếp tuyến cắt nhau tại K.
\(\Rightarrow KC=KM\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow KB=KC\)
△BME nội tiếp đường tròn (O) đường kính BE.
⇒△BME vuông tại MM.
\(\Rightarrow\widehat{BME}=90^0\)
b) Ta có: K thuộc đường trung trực của BM (\(KB=KM\))
O thuộc đường trung trực của BM \(\left(OB=OM\right)\)
⇒OK là đường trung trực của BM mà OK cắt BM tại N.
⇒N là trung điểm BM.
- Ta có: K thuộc đường trung trực của CM (\(KC=KM\))
I thuộc đường trung trực của CM \(\left(IC=IM\right)\)
⇒IK là đường trung trực của CM mà IK cắt CM tại P.
⇒P là trung điểm IK và \(CM\perp IK\) tại P.
Xét △BCM có: N là trung điểm BM, P là trung điểm CM.
⇒NP là đường trung bình của △BCM.
⇒NP//CM.
c) *Hạ \(IH\perp OB\) tại H.
Xét tứ giác BCIH có: \(\widehat{HBC}=\widehat{BCI}=\widehat{BHI}=90^0\)
⇒BCIH là hình chữ nhật.
\(\Rightarrow BC=IH;IC=BH=r\)
Xét △ICK vuông tại C có IP là đường cao:
\(\Rightarrow IK.IP=IC^2=r^2\)
Xét △OHI vuông tại H có:
\(HI^2+OH^2=OI^2\)
\(\Rightarrow HI=\sqrt{OI^2-OH^2}=\sqrt{\left(r+R\right)^2-\left(r-R\right)^2}=\sqrt{4Rr}=2\sqrt{Rr}\)
Mà \(BC=HI\Rightarrow BC=2\sqrt{Rr}\left(1'\right)\)
Ta có: \(2\sqrt{IM.IO-IK.IP}=2\sqrt{r\left(r+R\right)-r^2}=2\sqrt{Rr}\left(2'\right)\)
\(\left(1'\right),\left(2'\right)\Rightarrow BC=2\sqrt{IM.IO-IK.IP}\)

a: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: IO là phân giác của góc DIA
=>\(\widehat{DIA}=2\cdot\widehat{OIA}\)
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IO' là phân giác của góc AIE
=>\(\widehat{AIE}=2\cdot\widehat{AIO'}\)
Ta có: \(\widehat{DIA}+\widehat{EIA}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{OIA}+\widehat{O'IA}\right)=180^0\)
=>\(2\cdot\widehat{OIO'}=180^0\)
=>\(\widehat{OIO'}=90^0\)
b: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: ID=IA
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IA=IE
Ta có: IA=IE
ID=IA
Do đó: ID=IE
=>I là trung điểm của DE
=>I là tâm đường tròn đường kính DE
Xét ΔDAE có
AI là bán kính
\(AI=\dfrac{DE}{2}\)
Do đó: ΔADE vuông tại A
=>A nằm trên (I)
Xét (I) có
IA là bán kính
O'O\(\perp\)IA tại A
Do đó: OO' là tiếp tuyến của (I)
=>O'O là tiếp tuyến của đường tròn đường kính DE

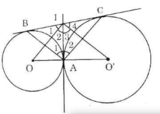
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
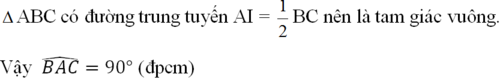
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
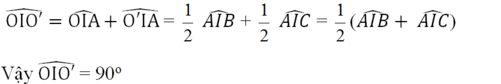
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)

1 2 1 2 3 4 B I C O A O'
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC .
Tam giác ABC có đường trung tuyến \(AI=\frac{1}{2}BC\)nên là tam giác vuông
Vậy \(\widehat{BAC}=90^o\left(đpcm\right)\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên :
\(\widehat{OIO'}=\widehat{OIA}+\widehat{O'IA}=\frac{1}{2}\widehat{AIB}+\frac{1}{2}\widehat{AIC}=\frac{1}{2}\left(\widehat{AIB}+\widehat{AIC}\right)\)
Vậy : \(\widehat{OIO'}=90^o\)
c) \(\Delta OIO'\) vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9 . 4 = 36
=> IA = 6 ( cm )
Vậy BC = 2 . IA = 2 . 6 = 12 (cm)

Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
O I O ' ^ = O I A ^ + O ' I A ^ = 1 2 A I B ^ + 1 2 A I C ^ = 1 2 A I B ^ + A I C ^
Vậy O I O ' ^ = 90 o

) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
A B C O' O I 4 9
Bài làm
a) Ta thấy: BC là tiếp tuyến chung ngoài và tiếp tuyến chung trong của hai đường tròn (O') và (O) cắt nhau tại I
=> CI = IA = IB (theo tính chất hai tiếp tuyến cắt nhau)
Xét tam giác ABC có: IA = 1/2BC
=> Tam giác ABC vuông tại A
Do đó: góc BAC = 90o (đpcm)
b) Ta thấy: O'I là tia phân giác của CO'O (theo tính chất hai tiếp tuyến cắt nhau)
=> \(\widehat{IO'O}=\frac{1}{2}\widehat{CO'O}\Rightarrow2\widehat{IO'O}=\widehat{CO'O}\)
Ta lại thấy: OI là tia phân giác của BOO' (theo tính chất hai tiếp tuyến cắt nhau)
=> \(\widehat{IOO'}=\frac{1}{2}\widehat{BOO'}\Rightarrow2\widehat{IOO'}=\widehat{BOO'}\)
Xét tứ giác O'CBO có:
\(\widehat{O'CB}+\widehat{CBO}+\widehat{B\text{OO}'}+\widehat{\text{OO}'C}=360^0\)(tổng 4 góc của tứ giác)
Hay \(90^0+90^0+2\widehat{IO'O}+2\widehat{IOO'}=360^0\)
=> \(2\left(\widehat{IO'O}+\widehat{IOO'}\right)=360^0-90^0-90^0=180^0\)
=> \(\widehat{IO'O}+\widehat{IOO'}=\frac{180^0}{2}=90^0\)\
Xét tam giác O'IO có:
\(\widehat{IO'O}+\widehat{IOO'}+\widehat{O'IO}=180^0\)(Tổng ba góc trong tam giác)
Hay \(90^0+\widehat{\text{OIO}'}=180^0\)
=> \(\widehat{\text{OIO}'}=180^0-90^0=90^0\)
Vậy góc OIO' = 90o
c) Xét tam giác O'IO vuông tại I có:
Đường cao IA
Theo hệ thức lượng trong tam giác:
Ta có: IA2 = OA * O'A
hay IA2 = 4 * 9
=> IA = 6 (cm)
Mà IA = IC = IB = 6 (cm)
=> IC + IB = BC
hay BC = 6 + 6 = 12 (cm)
Vậy BC = 12cm
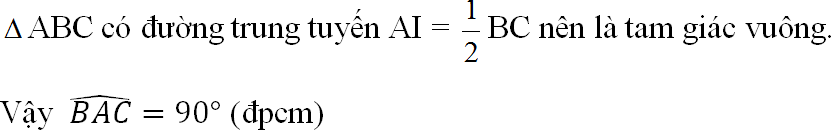
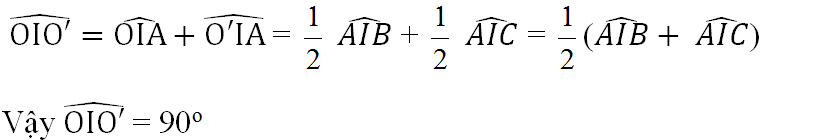
1: Sửa đề: góc BAC=90 độ
Xét (O) có
IB,IA là các tiếp tuyến
Do đó: IB=IA
Xét (O') có
IA,IC là các tiếp tuyến
Do đó: IA=IC
Ta có: IB=IA
IA=IC
Do đó: IB=IC
=>I là trung điểm của BC
Xét ΔABC có
AI là đường trung tuyến
\(AI=\dfrac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
2: Ta có: ΔACB vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
Xét tứ giác OBIA có \(\widehat{OBI}+\widehat{OAI}=90^0+90^0=180^0\)
nên OBIA là tứ giác nội tiếp
=>\(\widehat{OBA}=\widehat{OIA}\)
Xét tứ giác O'AIC có \(\widehat{O'AI}+\widehat{O'CI}=180^0\)
nên O'AIC là tứ giác nội tiếp
=>\(\widehat{O'IA}=\widehat{O'CA}\)
Ta có: \(\widehat{OBI}+\widehat{O'CI}=180^0\)
=>\(\widehat{OBA}+\widehat{CBA}+\widehat{BCA}+\widehat{O'CA}=180^0\)
=>\(\widehat{OBA}+\widehat{O'CA}=180^0-90^0=90^0\)
=>\(\widehat{OIA}+\widehat{O'IA}=90^0\)
=>\(\widehat{OIO'}=90^0\)