K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

6 tháng 4 2023
a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại E
=>OE*OA=OB^2=R^2

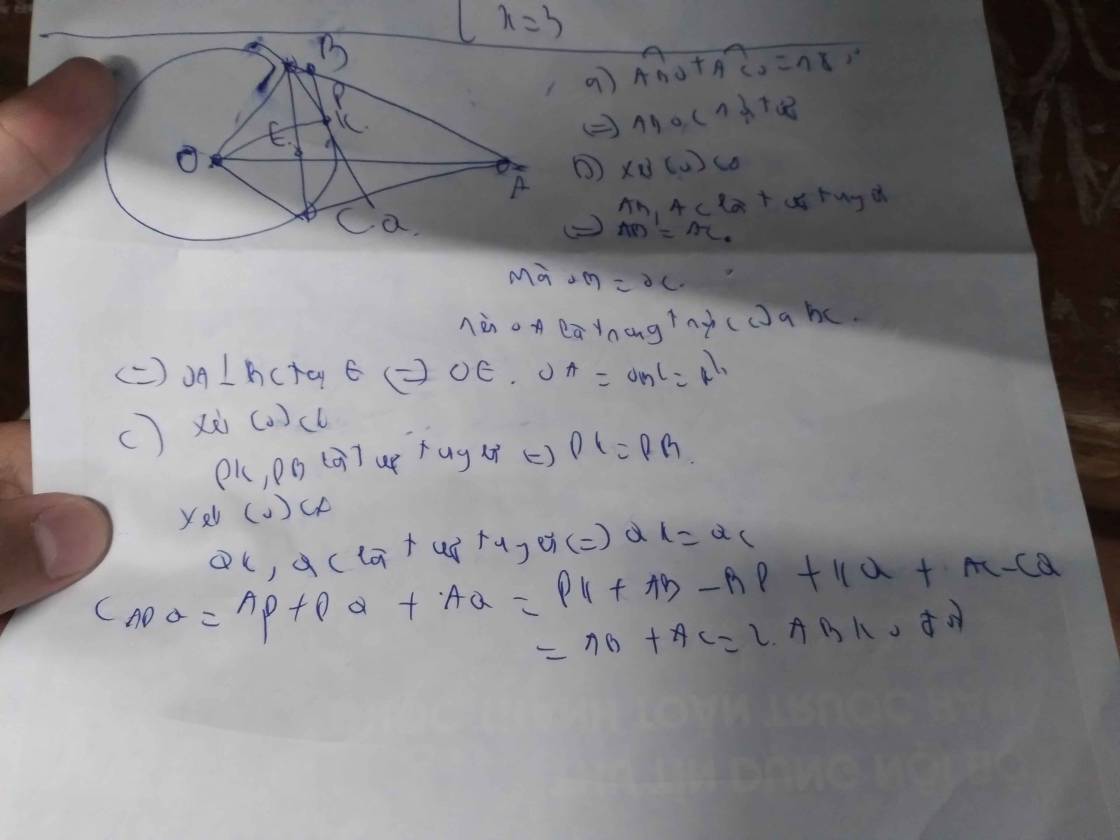
A B C O K P Q E M N
a) Vì AB là tiếp tuyến (O)
=> AB⊥OB
=> \(\widehat{ABO}\)\(=90^0\)
Vì AC là tiếp tuyến (O)
=> AC⊥OC
=>\(\widehat{ACO}\) \(=90^0\)
Ta có: \(\widehat{ABO}+\widehat{ACO}\) \(=90^0+90^0=180^0\)
=> Tứ giác ABOC nội tiếp đường tròn. (theo dấu hiệu nhận biết tứ giác nội tiếp)
b) Vì tiếp tuyến AB cắt tiếp tuyến AC tại A
\(\Rightarrow\left\{{}\begin{matrix}AB=AC\\BO=CO\end{matrix}\right.\)
\(\Rightarrow\) AO là đường trung trực ứng BC
\(\Rightarrow\) AO⊥BC ( mà E∈BC)
\(\Rightarrow\) BE⊥AO (đpcm)
Xét ΔABO có: \(\widehat{ABO}\) \(=90^0\) (cmtrn)
BE⊥AO (cmtrn)
\(\Rightarrow\) Áp dụng hệ thức lượng trong tam giác vuông.
\(\Rightarrow\) \(AO\cdot OE=OB^2\) (mà OB=R)
\(\Rightarrow OA\cdot OE=R^2\) (đpcm)
c) Vì tiếp tuyến BP cắt tiếp tuyến PK tại P
\(\Rightarrow PB=PK\)
Vì tiếp tuyến KQ cắt tiếp tuyến QC tại Q
\(\Rightarrow KQ=QC\)
Ta có: \(P_{APQ}=AP+PQ+AQ\) \(=AP+PK+KQ+AQ\)
\(\Leftrightarrow P_{APQ}=\left(AP+PB\right)+\left(QC+AQ\right)\)
\(\Leftrightarrow P_{APQ}=AB+AC\)
Vì \(AB+AC\) không thay đổi khi K chuyển động trên cung nhỏ BC
\(\Rightarrow\) Chu vi tam giác AQP không thay đổi khi K thay đổi trên cung nhỏ BC (đpcm).
d) Tự CM: \(\Delta MOP\sim\Delta NQO\)
\(\Rightarrow\frac{MP}{NO}=\frac{MO}{NQ}\) \(\Leftrightarrow MP\cdot NQ=MO\cdot NO=\frac{MN}{2}\cdot\frac{MN}{2}\)
\(\Leftrightarrow MP\cdot NQ=\frac{MN^2}{4}\)
\(\Leftrightarrow MN^2=4\cdot\left(MP\cdot NQ\right)\)
\(\Leftrightarrow MN=2\cdot\sqrt{MN\cdot NQ}\)
Áp dụng bđt Côshi ta có:
\(2\cdot\sqrt{MP\cdot NQ}\le MP+NQ\)
\(\Leftrightarrow MN\le MP+NQ\) (đpcm).
c) Xét ΔMAN có : \(\left\{{}\begin{matrix}AO\perp MN\\MO=NO=R\end{matrix}\right.\)
\(\Rightarrow\) Tam giác MAN cân tại A
\(\Rightarrow\) \(\widehat{M}=\widehat{N}\)
\(\Rightarrow\) \(\widehat{MAN}+2\widehat{M}\)\(=180^0\) (!)
Vì tiếp tuyến OB cắt tiếp tuyến OK tại P
\(\Rightarrow\) OP là phân giác \(\widehat{BOK}\)
\(\Rightarrow\) \(\widehat{BOP}=\widehat{POK}\)
Vì tiếp tuyến OK cắt tiếp tuyến OC tại Q
\(\Rightarrow\) \(\widehat{KOC}=\widehat{QOC}\)
Ta có: \(\widehat{BOP}+\widehat{POK}+\widehat{KOQ}+\widehat{QOC}=\widehat{BOC}\)
\(\Leftrightarrow\)\(2\widehat{POK}+2\widehat{KOQ}=\widehat{BOC}\)
\(\Leftrightarrow\) \(2\widehat{POQ}=\widehat{BOC}\)
Vì tứ giác ABOC nội tiếp đường tròn (cmtrn)
\(\Rightarrow\) \(\widehat{BAC}+\widehat{BOC}=\) \(180^0\)
\(\Leftrightarrow\) \(\widehat{MAN}+2\widehat{POC}\) \(=180^0\) (!!)
Từ (!)(!!) \(\Rightarrow\) \(\widehat{M}=\widehat{POC}\)
Vì \(\widehat{PON}\) là góc ngoài của ΔQOM
\(\Rightarrow\) \(\widehat{MPO}+\widehat{M}=\widehat{QON}\)
\(\Leftrightarrow\) \(\widehat{MPO}+\widehat{M}=\widehat{NOQ}+\widehat{POQ}\) (mà \(\widehat{M}=\widehat{POQ}\))
\(\Rightarrow\) \(\widehat{MPO}=\widehat{QON}\)
Xét ΔMOP∼ΔNQO vì :
\(\widehat{M}=\widehat{N}\) (cmtrn)
\(\widehat{MPO}=\widehat{QON}\) (cmtrn)