Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(AB=AC\Rightarrow\widehat{ABC}=\widehat{AEB}\) (hai góc nt chắn 2 cung bằng nhau)
Xét 2 tam giác ADB và ABE có:
\(\left\{{}\begin{matrix}\widehat{BAD}\text{ chung}\\\widehat{ABD}=\widehat{AEB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ADB\sim\Delta ABE\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AB}{AE}\Rightarrow AB^2=AD.AE\)

Nối BE, CE .
Vì AB=AC=> góc AEB= góc AEC. (1)
Vì tứ giác ABEC nội tiếp => góc ABC= góc AEC (2)
Kết hợp (1) và (2) => Góc AEB= góc ABC
Xét tam giác ABD và tam giác AEB có: góc ABC= góc AEB
góc BAE chung
=> 2 tam giác đồng dạng.
=> AB/AE= AD/AB => AB^2=AD.AE

Nối BE, CE .
Vì AB=AC=> góc AEB= góc AEC. (1)
Vì tứ giác ABEC nội tiếp => góc ABC= góc AEC (2)
Kết hợp (1) và (2) => Góc AEB= góc ABC
Xét tam giác ABD và tam giác AEB có: góc ABC= góc AEB
góc BAE chung
=> 2 tam giác đồng dạng.
=> AB/AE= AD/AB => AB^2=AD.AE

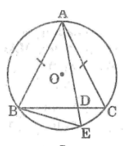

Chứng minh được: ∆ABD đồng dạng ∆AEB (g-g) => ĐPCM