Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: \(\widehat{ASC}=\dfrac{sđ\left(\widehat{AB}-\widehat{MC}\right)}{2}\) (1)
(\(\widehat{ASC}\) là góc có đỉnh nằm bên ngoài đường tròn (O)) và \(\widehat{MCA}=\dfrac{sđ\widehat{AM}}{2}\) (2)
(góc nội tiếp chắn cung \(\widehat{AM}\))
Theo giả thiết thì:
AB = AC => \(\widehat{AB}\) = \(\widehat{AC}\) (3)
Từ (1), (2), (3) suy ra:
\(\widehat{AB}-\widehat{MC}=\widehat{AC}-\widehat{MC}=\widehat{AM}\)
Từ đó \(\widehat{ASC}=\widehat{MCA}\).
góc ASC=1/2(sđ cung AB-sđ cung CM)
=1/2(sđ cung AC-sđ cung CM)
=1/2*sđ cungAM
góc MCA=1/2cung AM
=>góc ASC=góc MCA
( 1 số phần cơ bản sẽ làm tắt nha, cái đấy bạn sẽ tự trình bày rõ nhá, nhất là chứng minh tứ giác nội tiếp sẽ rút ngắn lại )
a)\(\widehat{ABO}=\widehat{AEO}=90^0\)
\(\Rightarrow ABEO\)nội tiếp
=> A,B,E,O thuộc 1 đường tròn
b) Xét tam giác AMC và tam giác ACN có:
\(\hept{\begin{cases}\widehat{NAC}chung\\\widehat{ACM}=\widehat{ANC}\left(=\frac{1}{2}sđ\widebat{MC}\right)\end{cases}\Rightarrow\Delta AMC~\Delta ACN\left(g-g\right)}\)
\(\Rightarrow\frac{AM}{AC}=\frac{AC}{AN}\)
\(\Rightarrow AC^2=AM.AN\)
c) \(\widehat{MJC}+\widehat{MFC}=180^0\)
\(\Rightarrow MJCF\)nội tiếp
\(\Rightarrow\widehat{MFJ}=\widehat{MCJ}\)
Mà \(\widehat{MCJ}=\widehat{MBC}\left(=\frac{1}{2}sđ\widebat{MC}\right)\)
\(\Rightarrow\widehat{MFJ}=\widehat{MBC}\left(1\right)\)
CMTT \(\widehat{MFI}=\widehat{MCB}\left(2\right)\)
Xét tam giác MBC có: \(\widehat{CMB}+\widehat{MCB}+\widehat{MBC}=180^0\left(3\right)\)
Từ (1), (2) và (3) \(\Rightarrow\widehat{CMB}+\widehat{MFJ}+\widehat{MFI}=180^0\)
\(\Rightarrow\widehat{CMB}+\widehat{PFQ}=180^0\)
\(\Rightarrow MPFQ\)nội tiếp
\(\Rightarrow\widehat{MPQ}=\widehat{MFQ}\)mà \(\widehat{MFQ}=\widehat{MBC}\left(cmt\right)\)
\(\Rightarrow\widehat{MPQ}=\widehat{MBC}\)mà 2 góc này ở vị trí đồng vị
\(\Rightarrow PQ//BC\)
d) Xét tam giác MIF và tam giác MFJ có:
\(\hept{\begin{cases}\widehat{MIF}=\widehat{MFJ}\left(=\widehat{MBF}\right)\\\widehat{MJF}=\widehat{MFI}\left(=\widehat{MCF}\right)\end{cases}\Rightarrow\Delta MIF~\Delta MFJ\left(g-g\right)}\)
\(\Rightarrow\frac{MI}{MF}=\frac{MF}{MJ}\)
\(\Rightarrow MI.MJ=MF^2\)
MI.MJ lớn nhất \(\Leftrightarrow MF^2\)lớn nhất
Mà \(MF=\frac{1}{2}MN\)
\(\Rightarrow MF^2=\frac{1}{4}MN^2\)
\(\Rightarrow MF\)lớn nhất <=> MN lớn nhất \(\Leftrightarrow MN\)là đường kính (O)
\(\Leftrightarrow M\)là điểm chính giữa cung BC
Vậy MI.MJ lớn nhất <=> M là điểm chính giữa cung BC.
( KO hiểu thì hỏi mình nha )
+ Đường tròn (O) có dây AB = AC
+
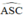là góc có đỉnh ngoài đường tròn chắn hai cung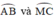 
Kiến thức áp dụng
+ Trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+ Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.