Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

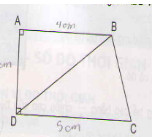
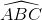 là góc tạo bởi hai tiếp tuyến BA và dây cung BC của (O). Dây BC = R suy ra
là góc tạo bởi hai tiếp tuyến BA và dây cung BC của (O). Dây BC = R suy ra![]() =
=  và
và  =
= 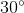 .
.
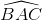 =
= 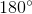 -
- 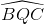 =
= 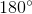 -
- 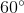 =
= 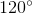 (tổng các góc của một tứ giác bằng
(tổng các góc của một tứ giác bằng 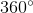 )
)

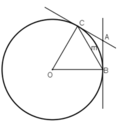
+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều

+ 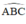 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC
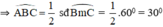
+ 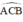 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB
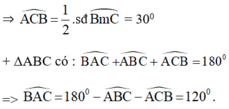

+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều

+ 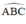 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC
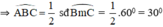
+ 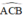 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB
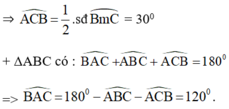

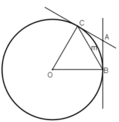
Xét tam giác OBA có OB = OC = BC = R
Vậy tam giác OAB là tam giác đều
=> ^BOC = ^OBC = ^OCB = 600
Vì AB ; AC là tiếp tuyến đường tròn (O) với B;C là tiếp điểm
=> ^OBA = ^OCA = 900
=> ^ABC = ^OBA - ^OBC = 900 - 600 = 300
Do AB = AC ( tc tiếp tuyến cắt nhau )
=> ^ABC = ^ACB = 300
=> ^BAC = 1800 - 2^ABC = 1200

a) vì AD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAD}=\widehat{DAC}\)\(\Rightarrow\)D là điểm chính giữa BC
\(\Rightarrow OD\perp BC\)
Mà \(DE\perp OD\)
\(\Rightarrow BC//DE\)
b) Ta có : \(\widehat{DAC}=\widehat{DCI}=\frac{1}{2}sđ\widebat{CD}\)
\(\Rightarrow\widehat{KAD}=\widehat{KCI}\)
suy ra tứ giác ACIK nội tiếp
c) OD cắt BC tại H
Dễ thấy H là trung điểm BC nên HC = \(\frac{BC}{2}=\frac{\sqrt{3}}{2}R\)
Xét \(\Delta OHC\)vuông tại H có :
\(HC=OC.\sin\widehat{HOC}\Rightarrow\sin\widehat{HOC}=\frac{HC}{OC}=\frac{\frac{\sqrt{3}}{2}R}{R}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{HOC}=60^o\)
\(\Rightarrow\widehat{BOC}=120^o\)
\(\Rightarrow\widebat{BC}=120^o\)
P/s : câu cuối là tính số đo cung nhỏ BC mà sao có cái theo R. mình ko hiểu. thôi thì bạn cứ xem đi nha.

a: góc OBA+góc OCA=180 độ
=>ABOC nội tiếp
b: Xét ΔOCB co OB=OC=BC
nen ΔOBC đều
=>góc OBC=60 độ
=>góc ABC=30 độ

a: xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
b: Xét ΔCAB vuông tại C có \(cosBAC=\frac{AC}{AB}=\frac12\)
nên \(\hat{BAC}=60^0\)
ΔACB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(CB^2=AB^2-AC^2=\left(2R\right)^2-R^2=4R^2-R^2=3R^2\)
=>\(CB=R\sqrt3\)
c: Xét (O) có
MC,MB là các tiếp tuyến
Do đó: MC=MB
=>M nằm trên đường trung trực của CB(1)
ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1),(2) suy ra MO là đường trung trực của CB
=>MO⊥CB
mà CA⊥CB
nên CA//OM
d: Gọi I là giao điểm của MA và CH, K là giao điểm của AC và MB
ΔACB vuông tại C
=>CA⊥CB tại C
=>CB⊥AK tại C
=>ΔKCB vuông tại C
Ta có: \(\hat{MCB}+\hat{MCK}=\hat{KCB}=90^0\)
\(\hat{MBC}+\hat{MKC}=90^0\) (ΔKCB vuông tại C)
mà \(\hat{MBC}=\hat{MCB}\) (ΔMBC cân tại M)
nên \(\hat{MCK}=\hat{MKC}\)
=>MC=MK
mà MC=MB
nên MB=MK(3)
ta có: KB⊥BA
CH⊥BA
DO đó: KB//CH
Xét ΔAMK có CI//MK
nên \(\frac{CI}{MK}=\frac{AI}{AM}\left(4\right)\)
Xét ΔAMB có IH//MB
nên \(\frac{IH}{MB}=\frac{AI}{AM}\) (5)
từ (3),(4),(5) suy ra CI=IH
=>I là trung điểm của CH
=>MA đi qua trung điểm I của CH

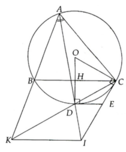
a, AD là phân giác B A C ^
=> D là điểm chính giữa B C ⏜ => OD ⊥ BC
Mà DE là tiếp tuyến => ĐPCM
b, E C D ^ = 1 2 s đ C D ⏜ = D A C ^ = B A D ^ => Đpcm
c, HC = P 3 2 => H O C ^ = 60 0 => B O C ^ = 120 0
=> l B C ⏜ = π . R . 120 0 180 0 = 2 3 πR

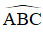 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC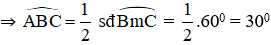
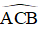 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB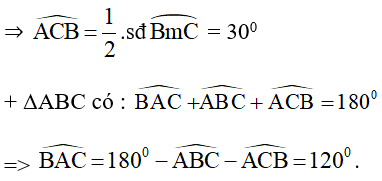
+ ΔOBC có OB = OC = BC (= R)
⇒ ΔOBC là tam giác đều
+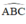 là góc tạo bởi tiếp tuyến BA và dây BC
là góc tạo bởi tiếp tuyến BA và dây BC
+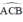 là góc tạo bởi tiếp tuyến AC và dây CB
là góc tạo bởi tiếp tuyến AC và dây CB
Kiến thức áp dụng
+ Trong một đường tròn, số đo của cung là số đo của góc ở tâm chắn cung đó.
+ Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.