Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Ta có \(\widehat{KAO}=\widehat{KMO}=90^o\) nên tứ giác KAOM nội tiếp.
2: Theo hệ thức lượng trong tam giác vuông ta có \(OI.OK=OA^2=R^2\)
3: Phần thuận: Dễ thấy H thuộc KI.
Ta có \(\widehat{AHO}=90^o-\widehat{HAI}=\widehat{AMK}=\widehat{AOK}\) nên tam giác AHO cân tại A.
Do đó AH = AO = R.
Suy ra H thuộc (A; R) cố định.
Phần đảo cm tương tự.
Vậy...

a: Xét tứ giác KAOM có
\(\widehat{KAO}+\widehat{KMO}=180^0\)
Do đó: KAOM là tứ giác nội tiếp
b: Xét (O) có
KA là tiếp tuyến
KM là tiếp tuyến
Do đó: KA=KM
hay K nằm trên đường trung trực của AM(1)
Ta có: OA=OM
nên O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OK là đường trung trực của AM
hay OK\(\perp\)AM
Xét ΔOAK vuông tại A có AI là đường cao
nên \(OI\cdot OK=OA^2\)

Mình chỉ nói gợi ý thôi, bạn tự phát triển nhé:
Câu a)
- CM: \(MO\)song song với \(NB\).
- CM: tam giác \(MAO\) và \(NOB\) bằng nhau.
- CM: \(OMNB\) là hình bình hành.
Câu b)
- CM: \(MAON\)là hình chữ nhật.
- CM: \(H\) là giao của \(MO\) và \(AN\)
- Gọi \(D\) là hình chiếu của \(H\) lên \(AB\). CM: \(D\) là trung điểm \(AO\).
- CM: \(H\) di động trên đường cố định.

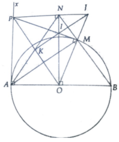
a, HS tự làm
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng