Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ \(BE\bot IK,CF\bot IK\)
Vì AK,AI là tiếp tuyến \(\Rightarrow\Delta AKI\) cân tại A \(\Rightarrow\angle AKI=\angle AIK\)
\(\Rightarrow\angle BKE=\angle CIF\)
Xét \(\Delta BEK\) và \(\Delta CFI:\) Ta có: \(\left\{{}\begin{matrix}\angle BKE=\angle CIF\\\angle BEK=\angle CFI=90\end{matrix}\right.\)
\(\Rightarrow\Delta BEK\sim\Delta CFI\left(g-g\right)\Rightarrow\dfrac{BE}{CF}=\dfrac{BK}{CI}\)
Vì BK,BH là tiếp tuyến \(\Rightarrow BH=BK\)
Vì CI,CH là tiếp tuyến \(\Rightarrow CI=CH\)
\(\Rightarrow\dfrac{BK}{CI}=\dfrac{BH}{CH}\Rightarrow\dfrac{BE}{CF}=\dfrac{BH}{CH}\)
Vì \(BE\parallel HD\parallel CF(\bot IK)\) \(\Rightarrow\dfrac{BH}{CH}=\dfrac{ED}{DF}\Rightarrow\dfrac{BE}{CF}=\dfrac{ED}{DF}\)
Xét \(\Delta BED\) và \(\Delta CFD:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{BE}{CF}=\dfrac{DE}{DF}\\\angle BED=\angle CFD=90\end{matrix}\right.\)
\(\Rightarrow\Delta BED\sim\Delta CFD\left(c-g-c\right)\Rightarrow\angle BDE=\angle CDF\)
mà \(\angle AKI=\angle AIK\Rightarrow\angle AKI-\angle BDE=\angle AIK-\angle CDF\)
\(\Rightarrow\angle ABD=\angle ACD\)
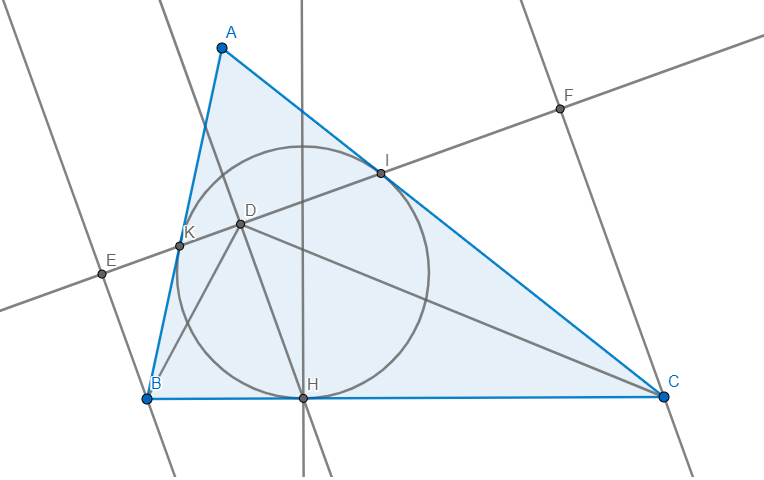

(O) tiếp xúc với BC, CA, AB tại H, I, K \Rightarrow OK vuông với KB ở K.
Mà HD vuông với KD ở D.
∠KBD=∠OKD∠KBD=∠OKD Hay ∠ABD=∠OKI∠ABD=∠OKI
Tương tự có ∠ACD=∠OIK∠ACD=∠OIK
(O) có ΔΔOIK cân ở O \Rightarrow ∠OKI=∠OIK
đó bạn nhé nhớ k nhe

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
A B C O I K H Q D
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

a) Tam giác ABC nội tiếp đường tròn (O) đường kính BC
=> OA=OB=OC và O là trung điểm của BC
=> Tam giác ABC vuông tại A
=> góc BAC = 90 độ
b) DO tam giác HAK nội tiếp đường tròn (I)
Lại có góc HAK = 90 độ
=> HK là đường kính của (I)
=> HK đi qua I
=> H,I,K thẳng hàng
c) Đề bài ghi ko rõ
d) 3 điểm nào?

A B C O H K I D E G 1 1 1
a, Xét \(\Delta BAC\)có OA = OB = OC ( = R )
=> \(\Delta BAC\)vuông tại A
\(\Rightarrow\widehat{BAC}=90^o\)
b, Xét \(\Delta AHO\) có IA = IH = IO (Bán kính (I))
=> \(\Delta AHO\)vuông tại H
=> \(\widehat{AHO}=90^o\)
Tương tự \(\widehat{AKO}=90^o\)
Tứ giác AHOK có 3 góc vuông nên là hcn
=> Trung điểm I của OA cũng là trung điểm của HK
Vì OA = OB ( = R )
=> \(\Delta AOB\)cân tại O
\(\Rightarrow\widehat{A_1}=\widehat{B_1}\)
Xét \(\Delta AHK\)vuông tại A có I là trung điểm HK
=> IA = IH
\(\Rightarrow\Delta AIH\)cân tại I
\(\Rightarrow\widehat{A_1}=\widehat{H_1}\)
Do đó \(\widehat{H_1}=\widehat{B_1}\)
=> HI // BC (so le trong)
Tương tự IK // BC
Do đó H , I , K thẳng hàng (tiên đề Ơ-clit)
c, Xét \(\Delta AOB\)cân tại O có OH là đường cao
=> OH là đường trung trực của AB
Mà điểm D thuộc OH
=> DA = DB
Tương tự EA = EC
Khi đó BD + CE = DA + EA = DE (DDpcm0+)
d,Gọi G là trung điểm DE
Mà tam giác DOE vuông tại D nên G là tâm (DOE)
Dễ thấy BD , CE là tiếp tuyến (O)
Nên BD , CE cùng vuông với BC
=> BD // CE
=> BDEC là hình thang
Mà GO là đường trung bình (dễ)
=> GO // BD
=> GO vuông với BC
Mà O thuộc BC
=> (DOE) tiếp xúc BC

a: góc KHB=1/2*180=90 độ
góc KAI+góc KHI=180 độ
=>KAIH nội tiếp
góc CHB=góc CAB=90 độ
=>CAHB nội tiếp
b: Xét ΔCIB có
CH,BA là đường cao
CH cắt BA tại K
=>K là trực tâm
=>IK vuông góc BC
c: Xét ΔIHC vuông tại H và ΔIAB vuông tại A có
góc I chung
=>ΔIHC đồng dạng với ΔIAB
=>IH/IA=IC/IB
=>IH*IB=IA*IC
pls help.