Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

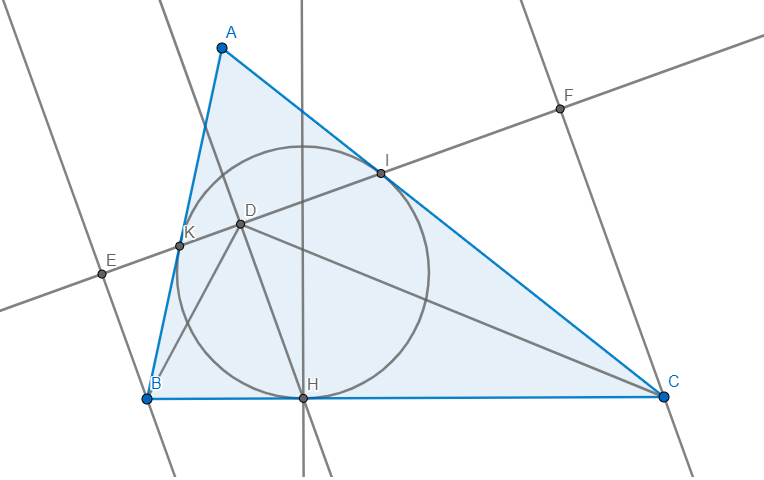
Kẻ \(BE\bot IK,CF\bot IK\)
Vì AK,AI là tiếp tuyến \(\Rightarrow\Delta AKI\) cân tại A \(\Rightarrow\angle AKI=\angle AIK\)
\(\Rightarrow\angle BKE=\angle CIF\)
Xét \(\Delta BEK\) và \(\Delta CFI:\) Ta có: \(\left\{{}\begin{matrix}\angle BKE=\angle CIF\\\angle BEK=\angle CFI=90\end{matrix}\right.\)
\(\Rightarrow\Delta BEK\sim\Delta CFI\left(g-g\right)\Rightarrow\dfrac{BE}{CF}=\dfrac{BK}{CI}\)
Vì BK,BH là tiếp tuyến \(\Rightarrow BH=BK\)
Vì CI,CH là tiếp tuyến \(\Rightarrow CI=CH\)
\(\Rightarrow\dfrac{BK}{CI}=\dfrac{BH}{CH}\Rightarrow\dfrac{BE}{CF}=\dfrac{BH}{CH}\)
Vì \(BE\parallel HD\parallel CF(\bot IK)\) \(\Rightarrow\dfrac{BH}{CH}=\dfrac{ED}{DF}\Rightarrow\dfrac{BE}{CF}=\dfrac{ED}{DF}\)
Xét \(\Delta BED\) và \(\Delta CFD:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{BE}{CF}=\dfrac{DE}{DF}\\\angle BED=\angle CFD=90\end{matrix}\right.\)
\(\Rightarrow\Delta BED\sim\Delta CFD\left(c-g-c\right)\Rightarrow\angle BDE=\angle CDF\)
mà \(\angle AKI=\angle AIK\Rightarrow\angle AKI-\angle BDE=\angle AIK-\angle CDF\)
\(\Rightarrow\angle ABD=\angle ACD\)

a, áp dụng t/c 2 tiếp tuyến cắt nhau suy ra góc bom =moa
xét tam giác cân OBAcó bom =moa suy ra oh vg ab
tứ giác đó nt do tổng 2 góc đối
b,cách mk là cm tam giác MEA đồng dạng vs MAF gg
đầu tiên bn nối I vs H Ta có IH là đg trung bình trong tam giác kab
=>IH// KB ,HAY GÓC IHA =CBA MÀ CBA =CEA =1/2 AC
=>TỨ GIÁC IHAE nt suy ra góc HEA CỘNG GÓC HIA =180 ĐỘ
GÓC HIA =BKA =90 ĐỘ
TỪ ĐÓ SUY RA GÓC HEA =90 ĐỘ HAY GÓC HEA LÀ GÓC VUÔNG
(O) tiếp xúc với BC, CA, AB tại H, I, K \Rightarrow OK vuông với KB ở K.
Mà HD vuông với KD ở D.
∠KBD=∠OKD∠KBD=∠OKD Hay ∠ABD=∠OKI∠ABD=∠OKI
Tương tự có ∠ACD=∠OIK∠ACD=∠OIK
(O) có ΔΔOIK cân ở O \Rightarrow ∠OKI=∠OIK
đó bạn nhé nhớ k nhe
bạn viết lại giùm mình đc ko, chứ mình ko thấy gì hết.