Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

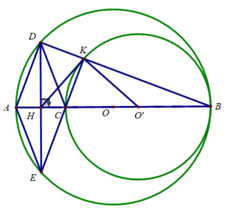
c) Ta có:
∠(CKB) = 90 0 (Góc nội tiếp chắn nửa đường tròn (O')) ⇒ CK ⊥ BD
∠(ADB) = 90 0 (Góc nội tiếp chắn nửa đường tròn (O)) ⇒ AD ⊥ BD
⇒ CK // AD
Lại có: CE // AD (Tứ giác ADCE là hình thoi)
⇒ C, E, K thẳng hàng

a, (O) và (I) tiếp xúc trong với nhau
b, Tứ giác ADCE là hình thoi
c, Có CK ⊥ AB, AD ⊥ DB
=> CK//AD mà CE//AD
=> B,K,D thẳng hàng
d, H K D ^ = H D K ^ ; I K B ^ = I B K ^
=> H K D ^ + I K B ^ = I B K ^ + H D K ^ = 90 0
=> I K H ^ = 90 0

Vi NN nằm trên (O)(O) nên ˆNAB=90∘NAB^=90∘(1) ⇒NB⊥DA⇒NB⊥DA. Mà DC⊥AB,AM⊥DBDC⊥AB,AM⊥DB ⇒K⇒K Là trực tâm tam giác DABDAB suy ra BK⊥ADBK⊥AD (2). Từ (1) và (2) suy ra B,N,KB,N,K thẳng hàng



Tam giác ABD nội tiếp trong đường tròn (O) có Ab là đường kính nên vuông tại D
Suy ra: AD ⊥ BD
Tứ giác ADCE là hình thoi nên EC // AD
Suy ra: EC ⊥ BD (1)
Tam giác BCK nội tiếp trong đường tròn (O’) có BC là đường kính nên vuông tại K
Suy ra: CK ⊥ BD (2)
Từ (1) và (2) suy ra EC trùng với CK
Vậy E, C, K thẳng hàng.