Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn làm bài:
Giả sử, gọi cạnh hình vuông là a và bán kính đường tròn là R.
Khi đó, chu vi hình vuông là 4a và chu vi hình tròn là 2πR.
Theo đề bài ra ta có: 4a=2πR⇒a=πR24a=2πR⇒a=πR2
Ta lập tỉ số diện tích hình vuông và hình tròn:
ShvShtr=a2πR2=(πR22)πR2=π2R24πR2=π4<1ShvShtr=a2πR2=(πR22)πR2=π2R24πR2=π4<1 (vì π ≈ 3,14)
⇒ Shv < Shtr
Vậy hình tròn có diện tích lớn hơn hình vuông
Hướng dẫn làm bài:
Ta có ˆA=12sđcungBC=600;ˆBDC=12.600=300A^=12sđcungBC=600;BDC^=12.600=300
Như vậy, điểm D tạo với hai mút của đoạn thẳng BC cố định một góc ˆBDC=300BDC^=300 nên D chuyển động trên cung chứa góc 30° dựng trên BC.
Ta có, khi A ≡ B thì D ≡ E và khi A ≡ C thì D ≡ C
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chưa góc 30° dựng trên BC

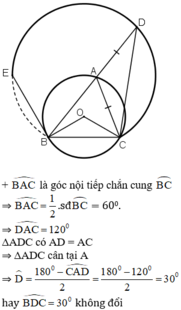
⇒ D nằm trên cung chứa góc 30 ° dựng trên đoạn BC.
+ Khi A ≡ C thì D ≡ C, khi A ≡ B thì D ≡ E (BE là tiếp tuyến của đường tròn (O) tại B).
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chứa góc 30 ° dựng trên BC.

A B C O D E K M F T y x
c) Gọi T là giao điểm thứ hai của FD với đường tròn (O). Ta c/m EO đi qua T.
Ta có: ^ADM = ^DAC + ^DCA = ^BAC/2 + ^ACB = ^BAD + ^MAB = ^MAD => \(\Delta\)DAM cân tại M => MA=MD
Lại có: MA và MF là 2 tiếp tuyến của (O) nên MA=MF. Do đó: MD=MF => \(\Delta\)MDF cân tại M (đpcm).
Dễ thấy: \(\Delta\)MAB ~ \(\Delta\)MCA (g.g) và \(\Delta\)MFB ~ \(\Delta\)MCF (g.g)
=> \(\frac{MA}{MC}=\frac{MF}{MC}=\frac{AB}{AC}=\frac{BD}{CD}=\frac{FB}{FC}\) => FD là tia phân giác ^BFC (1)
Kẻ tia đối Fy của FB => ^EFy = ^ECB = ^EBC = ^EFC => FE là phân giác ^CFy (2)
Từ (1) và (2) suy ra: FD vuông góc với FE (Vì ^BFC + ^CFy = 1800) hay ^EFT = 900
=> ET là đường kính của (O) => ET trùng với OE => OE đi qua T => ĐPCM.
d) Áp dụng ĐL Ptolemy có tứ giác BFCT nội tiếp có: BF.CT + CF.BT = BC.FT
=> CT.(BF+CF) = BC.FT => \(BF+CF=\frac{BC.FT}{CT}\le\frac{BC.ET}{CT}=\frac{2CK.ET}{CT}=2EC=2BE\)
Dấu "=" xảy ra khi F trùng với E <=> MF vuông góc OE <=> MF // BC => M không nằm trên BC (mâu thuẫn)
=> Không có dấu "=" => BF+CF < 2BE (đpcm).

a. Ta có: \(\widehat{ADB}=90^o\)(góc nội tiếp chắn nửa đường tròn) => \(\widehat{ADE}=90^o\)
Lại có: \(CH\perp AB\)tại H (gt) mà E \(\in CH\)(do E là giao điểm của BD và CH (gt)) => \(\widehat{EHA}=90^o\)
Xét tứ giác ADEH có: \(\widehat{ADE}+\widehat{EHA}=90^o+90^o=180^o\)=> tứ giác ADEH nội tiếp (DHNB) => đpcm
b.
Ta có: \(\widehat{ACB}=90^o\)(góc nội tiếp chắn nữa đường tròn) => \(\Delta ABC\)vuông tại C
=> \(S\Delta ABC=\frac{1}{2}AC\times BC=\frac{1}{2}CH\times AB\)=> CH = \(\frac{AC\times BC}{AB}\)
=> \(AC\times AH+CB\times CH=AC\times AH+CB\times\frac{AC\times BC}{AB}\)= \(AC\times(AH+\frac{BC^2}{AB})=AC\times\frac{(AH\times AB+BC^2)}{AB}\)(1)
Áp dụng hệ thức lượng trong \(\Delta ABC\)vuông tại C với đường cao CH ta được: AH \(\times AB=AC^2\)(2)
Áp dụng định lý pitago trong \(\Delta ABC\)vuông tại C ta được: \(AC^2+BC^2=AB^2\)(3)
Thế (2) và (3) vào (1) ta được : \(AC\times AH+CB\times CH=AB\times AC\)(ĐPCM)
c. Gọi K là điểm chính giữa cung AB (K nằm cùng phía với C so với bờ AB) => K là điểm cố định và \(KO\perp AB\)tại O => KO // CH => \(\widehat{KOC}=\widehat{KOM}=\widehat{HCO}\)(So le trong)
Nối K với M
Xét \(\Delta KOM\)và \(\Delta OCH\)có:
+ KO = OC = R
+ \(\widehat{KOM}=\widehat{HCO}\)(cmt)
+ OM = CH (gt)
=> \(\Delta KOM=\Delta OCH\)(c.g.c) => \(\widehat{KMO}=\widehat{OHC}=90^o\Rightarrow\Delta KOM\)vuông tại M => M \(\in(I,\frac{OK}{2})\)cố định (trong đó I là trung điểm của OK)
⇒ D nằm trên cung chứa góc 300 dựng trên đoạn BC.
+ Khi A ≡ C thì D ≡ C, khi A ≡ B thì D ≡ E (BE là tiếp tuyến của đường tròn (O) tại B).
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chứa góc 30º dựng trên BC.