Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác MBOC có \(\widehat{OBM}+\widehat{OCM}=90^0+90^0=180^0\)
nên MBOC là tứ giác nội tiếp
=>M,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
MB,MC là các tiếp tuyến
Do đó: MB=MC
=>M nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OM là đường trung trực của BC
=>OM\(\perp\)BC tại I và I là trung điểm của BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD tại C
Ta có: BC\(\perp\)CD
BC\(\perp\)OM
Do đó: CD//OM
c: Xét (O) có
ΔBHD nội tiếp
BD là đường kính
Do đó: ΔBHD vuông tại H
=>BH\(\perp\)HD tại H
=>BH\(\perp\)DM tại H
Xét ΔBDM vuông tại B có BH là đường cao
nên \(MH\cdot MD=MB^2\left(3\right)\)
Xét ΔMBO vuông tại B có BI là đường cao
nên \(MI\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(MH\cdot MD=MI\cdot MO\)
=>\(\dfrac{MH}{MO}=\dfrac{MI}{MD}\)
Xét ΔMHI và ΔMOD có
\(\dfrac{MH}{MO}=\dfrac{MI}{MD}\)
góc HMI chung
Do đó: ΔMHI đồng dạng với ΔMOD
=>\(\widehat{MIH}=\widehat{MDO}=\widehat{ODH}\)
mà \(\widehat{ODH}=\widehat{OHD}\)(ΔOHD cân tại O)
nên \(\widehat{MIH}=\widehat{OHD}\)

a: Ta có: ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(MA^2=15^2-9^2=144\)
=>\(MA=\sqrt{144}=12\left(cm\right)\)
Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{AO}{OM}=\dfrac{3}{5}\)
nên \(\widehat{AMO}\simeq36^052'\)
Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}\simeq73^044'\)
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=OC^2\)
Xét ΔOHE vuông tại H và ΔOKM vuông tại K có
\(\widehat{HOE}\) chung
Do đó: ΔOHE đồng dạng với ΔOKM
=>\(\dfrac{OH}{OK}=\dfrac{OE}{OM}\)
=>\(OK\cdot OE=OH\cdot OM\)
=>\(OK\cdot OE=OC^2\)
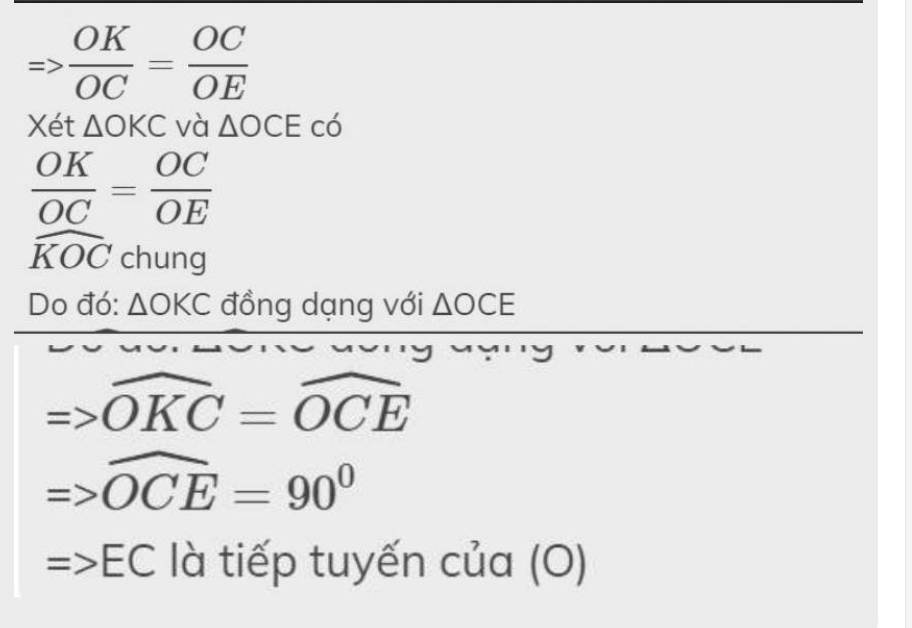
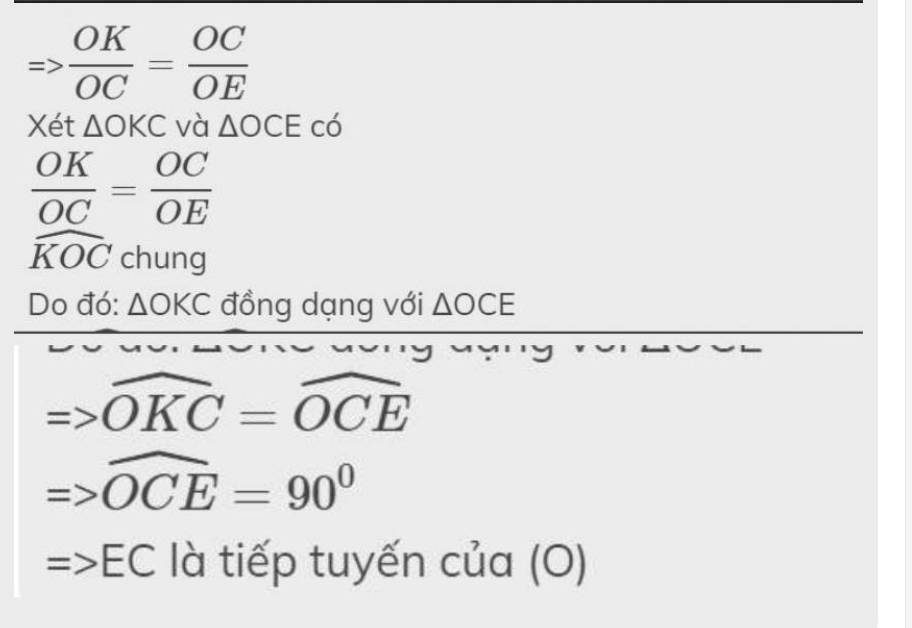
=>\(\dfrac{OK}{OC}=\dfrac{OC}{OE}\)
Xét ΔOKC và ΔOCE có
\(\dfrac{OK}{OC}=\dfrac{OC}{OE}\)
\(\widehat{KOC}\) chung
Do đó: ΔOKC đồng dạng với ΔOCE
=>\(\widehat{OKC}=\widehat{OCE}\)
=>\(\widehat{OCE}=90^0\)
=>EC là tiếp tuyến của (O)









câu 1 thì thg ngu cx lm đc
câu 2 CB' vuông góc niềm đau ak