Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, 700 góc nào bạn ?
b, Vì AB là tiếp tuyến (O) => ^ABO = 900
AO giao BC = K
AB = AC ; OB = OC = R
Vậy OA là đường trung trực đoạn BC
Xét tam giác ABO vuông tại B, đường cao BK
Áp dụng định lí Pytago tam giác ABO vuông tại B
\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm
Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm
Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm
Chu vi tam giác ABC là :
\(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm

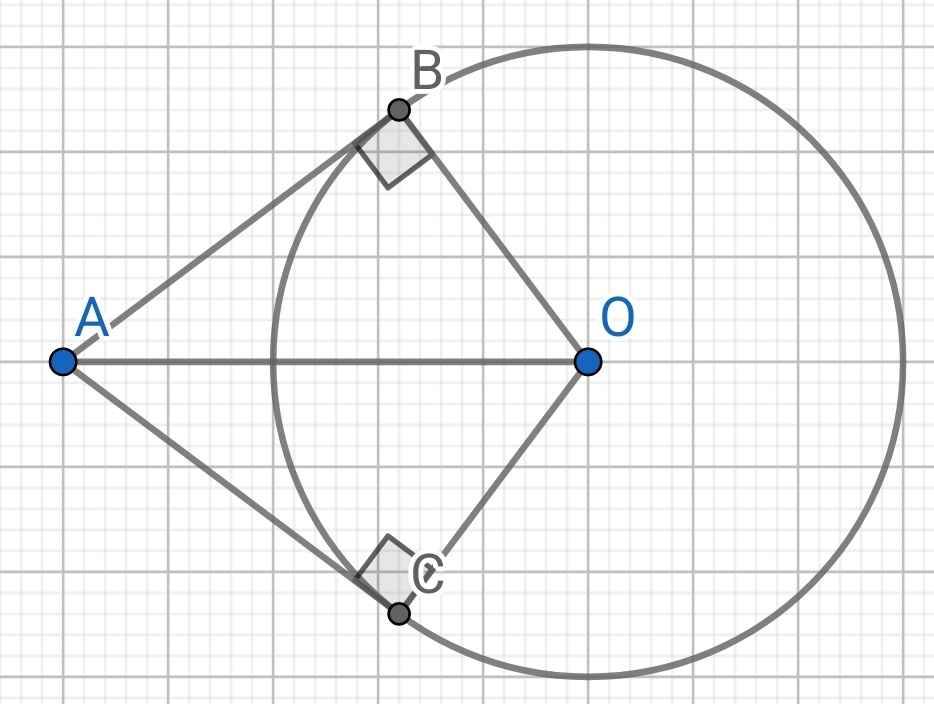
Từ một điểm A nằm bên ngoài đường tròn ( O ), kẻ các tiếp tuyến AB, AC với đường tròn ( B,C là các tiếp điểm )
a) Chứng minh rằng ABOC là tứ giác nội tiếp
b)Cho bán kính đường tròn ( O ) bằng 3cm, độ dài đoạn thẳng OA bằng 5cm. Tính độ dài đoạn thẳng BC
c) Gọi ( K ) là đường tròn qua A và tiếp xúc với đường thẳng BC tạo C. Đường trknf (K) và đường tròn (O ) cắt nhau tại điểm thứ hai là M. Chứng minh rằng đường thẳng BM đi qua trung điểm của đoạn thẳng AC

 ∆OAB vuông tại B
∆OAB vuông tại B
⇒ sinOAB = OB/OA = 6/10 = 3/5
⇒ ∠OAB ≈ 37⁰
Do AB và AC là hai tiếp tuyến cắt nhau
⇒ AO là tia phân giác của ∠BAC (tính chất hai tiếp tuyến cắt nhau)
⇒ ∠BAC = 2.∠OAB = 2.37⁰ = 74⁰
Do AB là tiếp tuyến \(\Rightarrow\Delta OAB\) vuông tại B
Đồng thời OA là phân giác \(\widehat{BAC}\Rightarrow\widehat{BAO}=\dfrac{1}{2}\widehat{BAC}=40^0\)
Trong tam giác vuông OAB:
\(sin\widehat{BAO}=\dfrac{OB}{OA}\Rightarrow OA=\dfrac{OB}{sin\widehat{BAO}}=\dfrac{10}{sin40^0}=15,56\left(cm\right)\)