Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AE’ = AF’, BD’ = BF’, CD’ = CE’ (tính chất hai tiếp tuyến cắt nhau).
Suy ra
AE’ + AF’ = (AC + CE’) + (AB + BF’)
= (AC + CD’) + (AB + BD’) = AC + BC + AB = 2p.
Do đó: AE’ = AF’ = p.

BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr (pp là chu vi của tam giác ABCABC, rr là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).

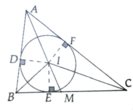
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b

a, Ta đã chứng minh được: AE = b + c - a 2
=> AE = a + b + c - 2 a 2 = p – a
∆AIE có IE = EA.tan B A C ^ 2
= (p – a).tan B A C ^ 2
b, Chú ý: BI ⊥ FD và CI ⊥ E. Ta có:
B I C ^ = 180 0 - I B C ^ + I C D ^ = 180 0 - 1 2 A B C ^ + A C B ^
= 180 0 - 1 2 180 0 - B A C ^ = 90 0 + B A C ^ 2
Mà: E D F ^ = 180 0 - B I C ^ = 90 0 - α 2
c, BH,AI,CK cùng vuông góc với EF nên chúng song song => H B A ^ = I A B ^ (2 góc so le trong)
và K C A ^ = I A C ^ mà I A B ^ = I A C ^ nên H B A ^ = K C A ^
Vậy: ∆BHF:∆CKE
d, Do BH//DP//CK nên B D D C = H P P K mà DB = DF và CD = CE
=> H P P K = B F C E = B H C K => ∆BPH:∆CPK => B P H ^ = C P E ^
Lại có: B F P ^ = C E F ^ => ∆BPF:∆CEP (g.g)
mà B P D ^ = C P D ^ => PD là phân giác của B P C ^