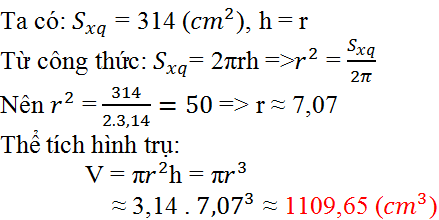Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)Gọi chiều dài ,chiều rộng ban đầu lần lượt là \(a,b\left(cm\right)\left(a,b>0\right)\)
Gọi diện tích ban đầu là \(S\left(cm^2\right)\left(S>0\right)\)
\(\Rightarrow ab=S\)
Theo đề bài,nếu tăng chiều rộng 2cm2cm và giảm chiều dài 11cm thì diện tích hình chữ nhật tăng 99cm22, nếu giảm chiều rộng 11cm và tăng chiều dài 22cm thì diện tích của hình chữ nhật không đổi.Khi đó,ta có hệ phương trình sau:
\(\Rightarrow\hept{\begin{cases}ab=S\\\left(a-1\right)\left(b+2\right)=S+9\\\left(a+2\right)\left(b-1\right)=S\end{cases}}\)
Ta có:(a-1)(b+2)=S+9
\(\Leftrightarrow ab+2a-b-2=S+9\)
\(\Leftrightarrow2a-b=11\left(1\right)\)(Do ab=S)
Ta lại có:(a+2)(b-1)=S
\(\Leftrightarrow ab+2b-a-2=S\)
\(\Leftrightarrow2b-a=2\left(2\right)\)(Do ab=S)
Từ (1) và (2)
\(\Rightarrow\hept{\begin{cases}2a-b=11\\2b-a=2\end{cases}\Leftrightarrow\hept{\begin{cases}2a-b=11\\4b-2a=4\end{cases}}}\)
\(\Rightarrow\left(2a-b\right)+\left(4b-2a\right)=11+4\)
\(\Leftrightarrow3b=15\)
\(\Leftrightarrow b=5\)
\(\Rightarrow a=\frac{b+11}{2}=\frac{5+11}{2}=8\)
Vậy chiều dài và chiều rộng của hình chữ nhật ban đầu là 8 cm và 5 cm

Diện tích xung quanh hình trụ bằng 314 c m 2
⇔ 2.π.r.h = 314
Mà r = h
⇒ 2 π r 2 = 31 ⇒ r 2 ≈ 50
⇒ r ≈ 7,07 (cm)
Thể tích hình trụ: V = π ⋅ r 2 h = π ⋅ r 3 ≈ 1109 , 65 cm 3
Kiến thức áp dụng
Hình trụ có bán kính đáy r, chiều cao h thì:
+ Diện tích xung quanh: Sxq = 2πrh
+ Thể tích: V = π.r2.h

Diện tích xung quanh hình trụ bằng 314cm2
⇔ 2.π.r.h = 314
Mà r = h
⇒ 2πr2 = 314
⇒ r2 ≈ 50
⇒ r ≈ 7,07 (cm)
Thể tích hình trụ: V = π.r2.h = π.r3 ≈ 1109,65 (cm3).

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3

a) Trong tam giác vuông BCH, ta có:
CH=BC.sinB^=12.sin60≈10,392 (cm)
Trong tam giác vuông ABC, ta có:
\(A\)=180−(60+40)=80
Trong tam giác vuông ACH, ta có:
\(AC=\dfrac{CH}{sinA}=\dfrac{10,932}{sin80}=10,552\left(cm\right)\)
b) Kẻ AK⊥BCAK⊥BC
Trong tam giác vuông ACK, ta có:
AK=AC.sinC≈10,552.sin40=6,783 (cm)
Vậy SABC=12.AK.BC≈12.6,783.12=40,696 (cm2)

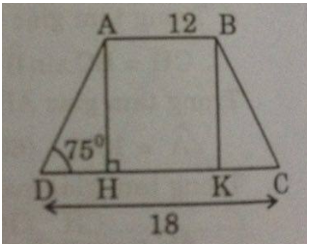
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, ˆD=75∘D^=75∘
Kẻ AH⊥CD,BK⊥CDAH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=