Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tự vẽ hình:)
Kẻ \(AH,CK\perp d\)
Xét \(\Delta vgAHB\)và \(\Delta vgCKB\)có
\(BC=BA\left(gt\right)\)
\(\widehat{ABH}=\widehat{CBK}\left(đ^2\right)\)
\(\Rightarrow\Delta ABH=\Delta CKB\left(ch-gn\right)\)
\(\Rightarrow CK=AH=2cm\)
Điểm C cách đg thg d 1 khoảng 2cm=>C di chuyển trên đg thg m // d và cách d 1 khoảng =2cm

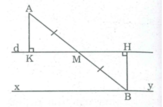
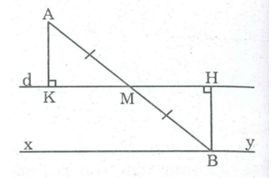
Kẻ AK ⊥ d,BH ⊥ d
Vì M thay đổi trên d, B đối xứng với A qua M nên AM = MB
Xét tam giác vuông AKM và BHM. Ta có: ∠ (AKM ) = ∠ (BHM ) = 90 0
AM = MB ( chứng minh trên)
∠ (AMK ) = ∠ (BMH ) ( đối đỉnh)
Do đó ∆ AKM = ∆ BHM ( cạnh huyền,góc nhọn) ⇒ AK = BH
Điểm A cố định, đường thẳng d cố định nên AK không đổi.
M thay đổi, B thay đổi cách đường thẳng d cố định một khoảng bằng AK không thay đổi nên B chuyển động trên đường thẳng xy song song với d và cách d một khoảng bằng AK.

Bài giải:
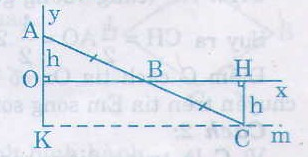
Kẻ AH và CK vuông góc với d.
Ta có AB = CB (gt)
ˆABHABH^ = ˆCBKCBK^ ( đối đỉnh)
nên ∆AHB = ∆CKB (cạnh huyền - góc nhọn)
Suy ra CK = AH = 2cm
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.

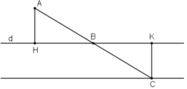
Gọi H, K là hình chiếu của A và C trên đường thẳng d.
⇒ Khoảng cách từ A đến d bằng AH
⇒ AH = 2cm.
Xét ΔAHB vuông tại H và ΔCKB vuông tại K có:
AB = BC
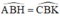
⇒ ΔAHB = ΔCKB (cạnh huyền – góc nhọn)
⇒ CK = AH = 2cm.
Vậy điểm C nằm trên đường thẳng song song với d, không đi qua A và cách d 2cm.

Lấy \(C\in a,C\ne B\), trên tia đối của tia \(CA\)lấy điểm \(N\)sao cho \(CN=\frac{1}{2}CA\).
Kẻ \(AK\perp MN,AK\)cắt \(BC\)tại \(H\).
Khi đó suy ra \(BC//MN\)
\(\frac{AK}{AH}=\frac{AM}{AB}=\frac{3}{2}\Rightarrow AK=\frac{3}{2}AH\).
Do đó điểm \(M\)luôn thuộc đường thẳng cố định (đường thẳng song song \(a\), khác phía với \(A\)cách \(a\)một khoảng \(\frac{1}{2}d\left(a,A\right)\).