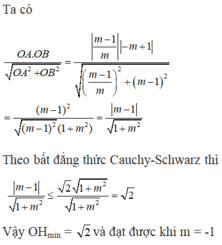Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(m-1)x+2m+1=y
=>(m-1)x-y+2m+1=0
\(d\left(O;d1\right)=\dfrac{\left|0\cdot\left(m-1\right)+0\cdot\left(-1\right)+2m+1\right|}{\sqrt{\left(m-1\right)^2+1}}=\dfrac{\left|2m+1\right|}{\sqrt{\left(m-1\right)^2+1}}\)
Để (d) lớn nhất thì \(\sqrt{\left(m-1\right)^2+1}_{Min}\)
=>m=1

\(y=m\left(2x+1\right)-3x-3\Leftrightarrow-m\left(2x+1\right)+3x+y+3=0\)
\(\Rightarrow\) đường thẳng luôn đi qua điểm cố định \(M\left(-\frac{1}{2};-\frac{3}{2}\right)\)
Gọi H là hình chiếu vuông góc của O lên đường thẳng
\(\Rightarrow OH=d\)
Theo định lý đường xiên - đường vuông góc ta luôn có:
\(OH\le OM\Rightarrow OH_{max}=OM\) khi \(H\equiv M\)
Mà \(OM=\sqrt{\left(-\frac{1}{2}\right)^2+\left(-\frac{3}{2}\right)^2}=\frac{\sqrt{10}}{2}\Rightarrow d=\frac{\sqrt{10}}{2}\)

Bạn kiểm tra lại đề, nếu x và y theo m đúng thế này thì \(xy\) chỉ có GTNN chứ không có GTLN

Gọi hoành độ M là a, do M thuộc \(\Delta\Rightarrow y_M=4-2a\Rightarrow M\left(a;4-2a\right)\)
\(\Rightarrow\overrightarrow{OM}=\left(a;4-2a\right)\) ; \(\overrightarrow{OA}=\left(1;-2\right)\)
\(\Rightarrow2\overrightarrow{OM}-\overrightarrow{OA}=2\left(a;4-2a\right)-\left(1;-2\right)=\left(2a-1;10-4a\right)\)
\(\Rightarrow\left|2\overrightarrow{OM}-\overrightarrow{OA}\right|=A=\sqrt{\left(2a-1\right)^2+\left(10-4a\right)^2}\)
\(\Rightarrow A=\sqrt{20a^2-84a+101}=\sqrt{20\left(a-\dfrac{21}{10}\right)^2+\dfrac{384}{5}}\ge\sqrt{\dfrac{384}{5}}\)
\(\Rightarrow A_{min}=\sqrt{\dfrac{384}{5}}\) khi \(a=\dfrac{21}{10}\)
\(\Rightarrow M\left(\dfrac{21}{10};\dfrac{-1}{5}\right)\)