Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A M → . A B → = A M . A B . cos A M → , A B →
= A M . A B . cos 0 ° = A M . A B .1 = A M . A B
ĐÁP ÁN B

À mk thiếu . Định m để đn thẳng AB và d có điểm chung
Bạn xem lại đề. Xác định $m$ để đoạn thẳng $AB$ có điểm chung là như thế nào thế?

13.
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|5.0-12.1-1\right|}{\sqrt{5^2+\left(-12\right)^2}}=1\)
6.
\(\overrightarrow{AB}=\left(-4;2\right)=-2\left(2;-1\right)\)
Phương trình AB:
\(1\left(x-1\right)+2\left(y-2\right)=0\Leftrightarrow x+2y-5=0\)
Phương trình giao điểm: \(\left\{{}\begin{matrix}x+2y-5=0\\4x-7y+m=0\end{matrix}\right.\) \(\Rightarrow y=\frac{m+20}{15}\)
Để đường thẳng và đoạn AB có điểm chung
\(\Leftrightarrow2\le\frac{m+20}{15}\le4\Rightarrow10\le m\le40\)

Tham khảo:
a) Điểm M thuộc đường thẳng d khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng phương (cùng giá d)
Khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \).
Vậy khẳng định a) đúng.
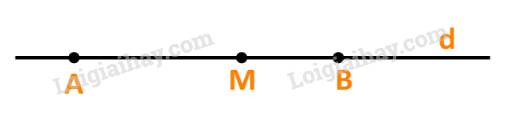
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
Sai vì \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \) khi và chỉ khi \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng hướng.
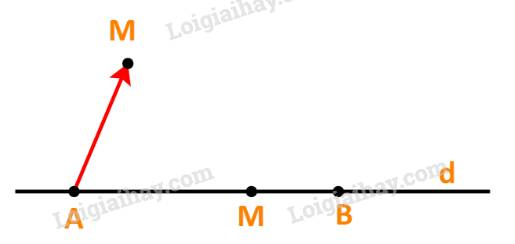
c) Điểm M thuộc tia đối của tia AB, tức là A nằm giữa M và B.
Khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) ngược hướng
\( \Leftrightarrow \) tồn tại số \(t \le 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
Vậy khẳng định c) đúng.


Đáp án A
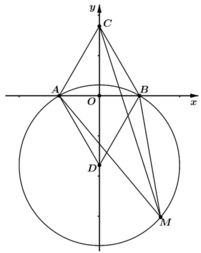
Chọn hệ trục Oxy sao cho Ox trùng với AB , chiều dương hướng từ A đến B ,trục Oy là đường trung trực của đoạn AB =>
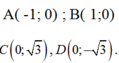
Phương trình đường tròn tâm D qua A; B là:
![]()
Giả sử M(a;b) là điểm bất kì trên đường tròn .Ta có :
MA2= (a+ 1) 2+ b2
MB2= (a-1) 2+ b2
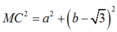

+ M nằm trên đường tròn (1) nên : 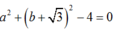
=> MA2+ MB2= MC2
=> MA; MB; MC là độ dài ba cạnh của một tam giác vuông.

Lời giải:
\(\overrightarrow{AB}=(-4,2)\)
\(\overrightarrow{u_d}=(2,-1)\)
Để 2 đường thẳng cắt nhau thì \(\frac{-4}{2}\neq \frac{2}{-1}\) (vô lý)
Do đó 2 đường thẳng không thể cắt nhau với mọi $m$. Đáp án D
PTTQ của d : \(1\left(x-m\right)+2\left(y-1\right)=0\)
\(\Leftrightarrow x+2y-m-2=0\)
Để d cắt AB thì A và B nằm khác phía so với d hoặc là một trong 2 điểm A và B nằm trên d . Nên ta có :
\(\left(1+4-m-2\right)\left(-3+8-m-2\right)\le0\)
\(\Leftrightarrow\left(-m+3\right)\left(-m+3\right)\le0\)
\(\Leftrightarrow m=3\)
Chọn B

M A → . M B → = M A . M B . cos M A → , M B →
= M A . M B . cos 180 ° = M A . M B . − 1 = − M A . M B
Chọn C