
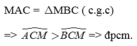
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

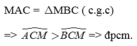

Xét ΔCMA vuông tại M và ΔCMB vuông tại M có
CM chung
MA=MB
Do đó: ΔCMA=ΔCMB
=>\(\widehat{ACM}=\widehat{BCM}\)
=>CM là phân giác của góc ACB

Ta có: M1^ + M2^ = 180o hay M1^ + 90o = 180o
=> M1^ = 180o - 90o = 90o
=> M1^ = M2^ = 90o
Xét ΔKAM và ΔKBM có:
KM Cạnh chung
M1^ = M2^ = 90o (cmt)
AM = BM (gt)
=> ΔKAM = ΔKBM (c.g.c)
=> K1^ = K2^ (2 góc tương ứng)
=> KM là tia phân giác của AKB^ (ĐPCM)
C A B M
Bài làm
Xét tam giác CAM và tam giác ABM có:
AM = MB ( Do M là trung điểm AB )
/ CMA = / CMB ( cùng = 90o )
CM chung
=> Tam giác CAM = tam giác ABM ( c.g.c )
=> CA = CB ( hai cạnh tương ứng )
=> Tam giác CAB cân tại C
Vì tam giác CAM = tam giác ABM ( cmt )
=> / ACM = / BCM ( hai góc tương ứng )
=> CM là tia phân giác của góc ACB ( đpcm )

bạn tự vẽ hình nhé
Xét tam giác vuông ACM và tam giác vuông BCM có
\(AM=BM\left(Gt\right)\)
CM chung
=> tam giác vuông ACM = tam giác vuông BCM (T/C tam giác vuông )
=> \(\widehat{ACM}=\widehat{BCM}\)(2 góc tương ứng)
=> CM là tia phân giác của \(\widehat{ACB}\)

tôi chịu có ai biết thì giúp đi tôi cũng đang cần lời giải của bài đó ạ