Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm
Hướng dẫn:
Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm

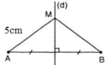
Điểm M thuộc đường trung trực của AB
⇒ MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm

M thuộc đường trung trực của đoạn thẳng AB =>điểm M cách đều 2 đầu mút của đoạn AB=>MA=MB
Mà MA=5cm
=>MB=5cm

Đặt AB vương góc với đường trung trực tại E
xét 2 TG AME và BME, ta có
AE=BE (gt) AEM=BEM=90 độ ME cạnh chung
suy ra TG AME=TG BME (cgc)
suy ra MA=MB


A B M C D E x
a) Mx\(⊥\)AB, C\(\in\)Mx, MC=MA \(\Rightarrow\)\(\Delta\)AMC vuông cân tại M \(\Rightarrow\)\(\widehat{MAC}=\widehat{MCA}=45^0\)
Tương tự \(\Delta\)BMD vuông cân tại M\(\Rightarrow\widehat{MBD}=\widehat{MDB}=45^0\)
\(\Rightarrow\widehat{MAC}=\widehat{MDB}=45^0\)hay \(\widehat{MAC}=\widehat{CDE}=45^0\)
\(\Rightarrow\Delta CED\)vuông cân tại E \(\Rightarrow AE⊥BD\)(đpcm)
b) BD \(⊥\)AC tại E, MD\(⊥\)AB => D là trực tâm của \(\Delta\)ABC.
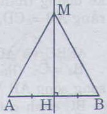
C. MA=MB=2,5cm.
C