Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có Um không đổi và để UAm luôn không đổ vs mọi gtri của R thì : Um=UAm hay ZL=2ZC =2.100=200 → L=2/π ( D)
Sử dụng hình vẽ suy luận cho nhanh : R ZL ZC UAm Um

Ta có:
Con lắc thực hiện 100 dao động hết 31,4 (s)
Lại có gốc thời gian là lúc quả cầu có li độ 2cm và đang chuyển động theo chiều dương của trục tọa độ với vận tốc có độ lớn
và

Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)
Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng
Ta có: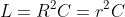
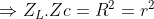
Điện áp hiệu dụng của đoạn mạch RC gấp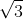 lần điện áp hiệu dụng hai đầu cuộn dây
lần điện áp hiệu dụng hai đầu cuộn dây



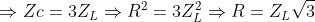

=> Hệ số công suất của đoạn mạch là