Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

9. Trên một đường thẳng, tại hai điểm A và B cách nhau 10 km, có hai ô tô xuất phát cùng lúc và chuyển động cùng chiều. Ô tô xuất phát từ A có tốc độ 60 km/h và ô tô xuất phát từ B có tốc độ 40 km/h.
a) Lấy gốc tọa độ ở A, gốc thời gian là lúc xuất phát, hãy viết công thức tính quãng đường đi được và phương trình chuyển động của hai xe.
b) Vẽ đồ thị tọa độ - thời gian của hai xe trên cùng một hệ trục (x, t).
c) Dựa vào đồ thị tọa độ - thời gian để xác định vị trí và thời điểm mà xe A đuổi kịp xe B.
Trả lời:
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị
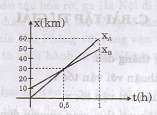
c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị

c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.

a) Công thức tính quãng đường đi được của 2 xe là :
SA = VA.t = 60t và SB = VB.t = 40t.
Phương trình chuyển động của 2 xe:
xA = 0 + 60t và xB = 10 + 40t
Với S và x tính bằng km; t tính bằng giờ.
b)
| t(h) |
0 |
0,5 |
1 |
2 |
3 |
... |
| xA (km) |
0 |
30 |
60 |
120 |
180 |
... |
| xB (km) |
10 |
30 |
50 |
90 |
130 |
... |
c) Khi 2 xe gặp nhau thì tọa độ của chúng bằng nhau:
xA = xB
60t = 10 + 40t
⇒ 20t = 10
⇒ t = 0,5 h
⇒ xA = 60.0,5 = 30 km.
Vậy điểm gặp nhai cách gốc tọa độ A một đoạn 30 km.
Trên đồ thị điểm gặp nhai có tọa độ (t,x ) tương ứng là (0,5;30).

1. PT chuyển động thẳng biến đổi đều có dạng:
\(x=x_0+v_0t+\dfrac{1}{2}a.t^2\)
Đối chiếu với phương trình trên ta được:
\(v_0=10\left(\dfrac{m}{s}\right)\)
\(a=8\left(\dfrac{m}{s^2}\right)\)
PT vận tốc: \(v=v_0+a.t=10+8.t\)
Thay \(\text{ t=2s}\) vào pt trên ta được: \(\text{v=10+8.2=26(m/s)}\)
2. 18km/h=5m/s
ta có: v5 = 5 + 5a
v4 = 5 + 4a
=> v5^2-v4^2=2.a.S
=> 9a^2 + 10a = 11,8a
=> a=0 (loại) hoặc a=0,2
=> a=0,2 m/s^2

1\(\Rightarrow v=20km/h=\dfrac{50}{9}m/s\)
2.\(\Rightarrow S=vt=20.2=40km\)
3.\(\Rightarrow80=10+20t=>t=3,5h\)
4.

a) Gốc tọa độ lấy ở H. Gốc thời gian là lúc xe xuất phát từ H.
Công thức tính quãng đường đi của ô tô:
∗ Trên quãng đường H – D: S1 = 60t (x: km; t: h) với x ≤ 60 km tương ứng t ≤ 1 h.
∗ Trên quãng đường D – P: Do ô tô dừng lại 1h cộng với thời gian chuyển động từ H → D hết 1h nữa nên ô tô trễ 2h so với mốc thời gian đã chọn lúc xuất phát từ H. Ta có: S2 = 40.(t - 2) (km, h) với điều kiện t ≥ 2.
∗ Phương trình chuyển động của ô tô trên đoạn HD: x1 = 60t với x ≤ 60 km.
Trên đoạn D – P: x2 = 60 + 40(t - 2) với x ≥ 60 km, t ≥ 2h.
b) Đồ thị
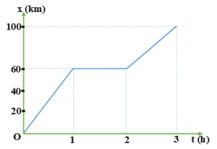
c) Trên đồ thị ta xác định được thời điểm xe đến P là 3h
d) Kiểm tra bàng phép tính:
Thời điểm ô tô đến P:
![]()
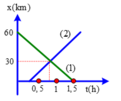
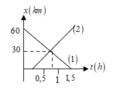
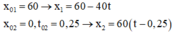
 tham khảo nếu sai thì thôi :v
tham khảo nếu sai thì thôi :v
Chọn đáp án C
? Lời giải:
x 01 = 60 → x 1 = 60 − 40 t ; x 02 = 0 , t 02 = 0 , 25 → x 2 = 60 t − 0 , 25