Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

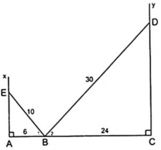
Áp dụng định lý Py – ta –go và tam giác CDB vuông tại C ta được:
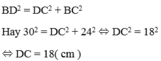
Xét Δ BEA và Δ DBC có:
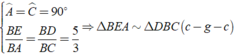
Từ định nghĩa về tam giác đồng dạng và tính chất về góc của tam giác vuông DCB. Ta có: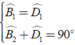
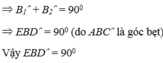

vì góa A=B=C=90 độ
=>ABCD là hình chữ nhật
mà AB=AC
=>ABCD là hình vuông=>AD vuông góc BC

a: góc A=180-60=120 dộ
=>góc EAB=60 độ=góc BAI
Xet ΔEAB và ΔIAB có
góc EAB=góc IAB
AB chung
EA=IA
=>ΔEAB=ΔIAB
=>BE=BI
=>AB là trung trực của IE
Chứng minh tương tự, ta được: AC là trung trực của IF
b: góc EAB=góc FAC=60 độ
=>góc EAB+góc BAI=góc FAC+góc IAC
=>góc EAI=góc FAI
Xét ΔEAI và ΔFAI có
AI chung
góc EAI=góc FAI
AE=AF
=>ΔEAI=ΔFAI
=>EI=FI
=>ΔIFE cân tại I
=>góc EIF=2*góc AIE
ΔEAI cân tại A
=>góc AIE=(180-60-60)/2=30 độ
=>góc EIF=60 độ
=>ΔIEF đều
c: góc AIE=góc AIF
=>AI là phân giác của góc EIF
mà ΔEIF đều
nên AI vuông góc EF

Gọi giao của CO với DB là E
a: Xét ΔOAC vuông tại A và ΔOBE vuông tại B có
OA=OB
góc AOC=góc BOE
=>ΔOAC=ΔOBE
=>AC=BE và OD=OE
Xét ΔACO vuông tại A và ΔBDO vuông tại B có
góc ACO=góc BDO(=góc DCO)
=>ΔACO đồng dạng với ΔBDO
b: Xét ΔDCE có
DO vừa là đường cao, vừa là trung tuyến
=>ΔDCE cân tại D
=>DE=DC
=>DC=DB+BE=DB+AC
c; Xét ΔNAC vàΔNDB có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔNAC đồng dạng với ΔNDB
=>NA/ND=AC/BD=CM/MD
=>MN//AC

A C B D x y O
1) Xét tứ giác ABCD có :
\(\hept{\begin{cases}BD//AC\left(Bx//AC\right)\\AB//CD\left(AB//Cy\right)\end{cases}}\)=> ABCD là hình bình hành
=> AB = CD
2) Vì ABCD là hình bình hành
=> AD và BC cắt nhau tại trung điểm của mỗi đường ( Tính Chất )
Mà O là trung điểm của BC
=> O là trung điểm của AD
=> O , A , D thẳng hàng ( Đpcm )