Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

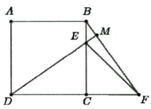
Chứng minh được:
C B F ^ + B E M ^ = M D F ^ + D E C ^ = 90 0
=> B M D ^ = 90 0 nên M thuộc đường tròn đường kính BD. Mà E Î BC nên quỹ tích của điểm M là là cung B C ⏜ của đường tròn đường kính BD

A B C D M N F O E I J x
a) Xét \(\Delta\)ABM và \(\Delta\)ADN có: ^ABM = ^ADN (=900); AB=AD; BM=DN => \(\Delta\)ABM = \(\Delta\)ADN (c.g.c)
=> AM=AN (2 canh tương ứng); ^BAM = ^DAN (2 góc tương ứng). Mà ^BAM + ^DAM = 900
=> ^DAN + ^DAM = ^MAN = 900 => AM vuông góc AN
Ta có: MF//AN; NF//AM; AM vuông góc AN nên ^MAN = ^AMF = ^ANF = 900
Do đó: Tứ giác ANFM là hình chữ nhật. Lại có: AM=AN (cmt) => Tứ giác ANFM là hình vuông (đpcm).
b) Gọi I và J lần lượt là hình chiếu của F trên 2 đường thẳng CD và BC
Tứ giác ANFM là hình vuông => FM=FN
Xét tứ giác CNFM có: ^MCN = ^MFN = 900 => ^FNC + ^CMF = 1800 => ^FNC = ^FMJ hay ^FNI = ^FMJ
Xét \(\Delta\)FIN và \(\Delta\)FJM có: ^FIN = ^FJM (=900); FN=FM; ^FNI = ^FMJ
=> \(\Delta\)FIN = \(\Delta\)FJM (Ch.gn) => FI = FJ (2 cạnh tương ứng)
Xét ^MCN: Có FI và FJ là k/c từ điểm F tới 2 cạnh của góc này; FI=FJ
=> F nằm trên đường phân giác của ^MCN (đpcm).
c) Gọi giao điểm của tia AD và CF là E.
CF là phân giác ^MCN => ^FCN = ^MCN/2 = 450 => ^FCN = ^ACD = 450
=> \(\Delta\)ACE vuông tại C có đường phân giác CD. Mà CD vuông góc AE
=> \(\Delta\)ACE vuông cân tại C = >CD đồng thời là đường trung tuyến => D là trung điểm AE
Suy ra: OD là đường trung bình \(\Delta\)FAE => OD // EF hay OD // CF (1)
Dễ c/m: BD // CF (Do ^DBC + ^BCF = 450 + 1350 = 1800) (2)
Từ (1) và (2) => 3 điểm B;D;O thẳng hàng (đpcm).
d) Ta thấy: B;D;O là 3 điểm thẳng hàng; BD cố định nên O luôn thuộc đường thẳng BD cố định khi M di động trên Cx.

a) Chưa có điều kiện để xác định được điểm N
b) Em tham khảo tại đây nhé.
Câu hỏi của Hàn Hy - Toán lớp 9 - Học toán với OnlineMath


Gọi \(H\) là hình chiếu vuông góc của \(B\) lên đường thẳng \(d\). Suy ra \(H\) là điểm cố định. Qua \(H\) vẽ hai đường thẳng \(d_1,d_2\) vuông góc với nhau và tạo với \(d\) một góc \(45^{\circ}\). Suy ra \(d_1,d_2\) là các đường thẳng cố định.
Ta thấy năm điểm \(A,B,C,D,H\) cùng nằm trên một đường tròn có đường kính \(BD\). Suy ra tứ giác \(ABCH\) nội tiếp. Do đó \(\angle BHC=\angle BAC=45^{\circ}.\) Vậy \(C\) thuộc \(d_1\) hoặc \(d_2\).
Đảo lại với mỗi điểm \(C\) thuộc \(d_1\) hoặc \(d_2\). Qua \(C\) vẽ đường thẳng vuông góc với BC cắt \(d\) ở \(D\). Vì \(\angle BHD=\angle BCD\left(=90^{\circ}\right)\) nên tứ giác \(DBCH\) nội tiếp. Thành thử \(\angle BDC=\angle BHC=45^{\circ}\). Do đó tam giác \(BCD\) vuông cân. Suy ra \(C\) là một đỉnh của hình vuông với đường chéo \(BD\). (ĐPCM)