Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

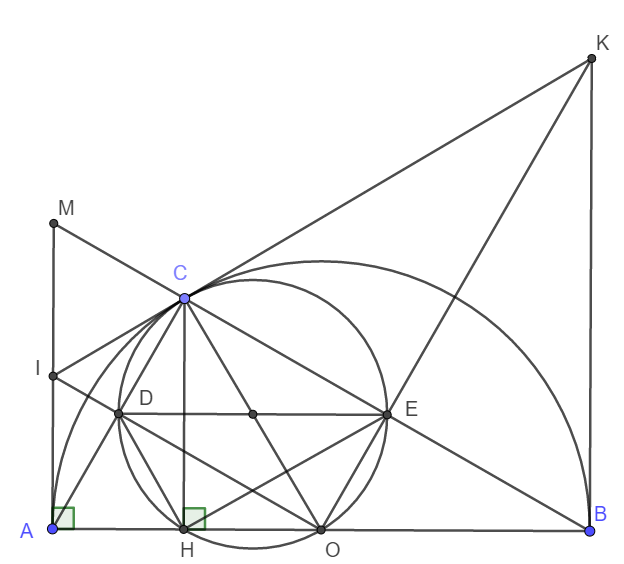
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.
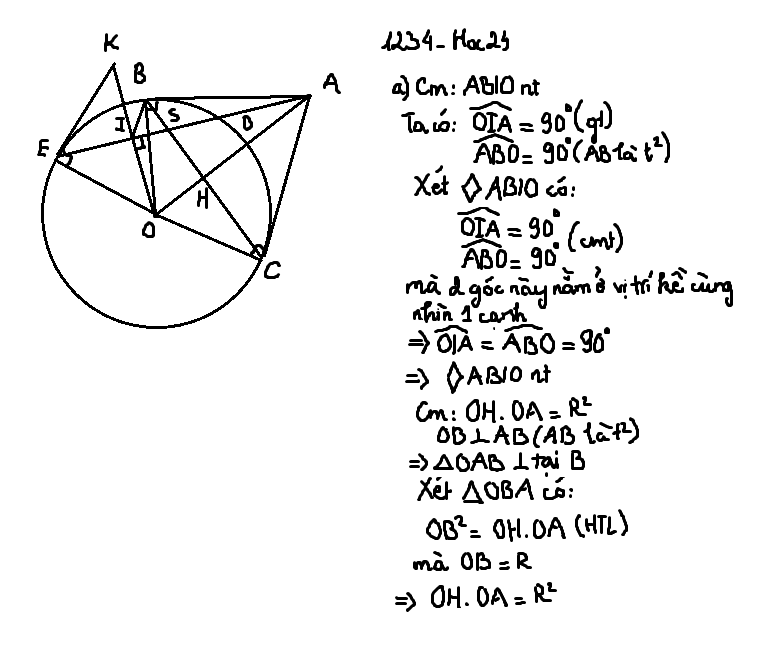

( Mình nhắc trước có một số chỗ mình viết tắt ^^ vì bài dài đánh chữ nhiều cũng mỏi lắm, với cả chỗ viết tắt cũng cơ bản í mà :)) ko hiểu chỗ nào thì hỏi nha )
a) Vì \(\hept{\begin{cases}AB\perp OB\\OI\perp DE\end{cases}\Rightarrow\hept{\begin{cases}\widehat{ABO}=90^0\\\widehat{AIO}=90^0\end{cases}}}\)
Xét tứ giác ABIO có: \(\widehat{ABO}=\widehat{AIO}\left(=90^0\right)\)
Mà 2 đỉnh B,I cùng nhìn cạnh OA dưới 1 góc vuông
\(\Rightarrow ABIO\)nội tiếp ( dhnb )
+) Ta có: \(\hept{\begin{cases}\widehat{ABH}=\frac{1}{2}sđ\widebat{BC}\\\widehat{BOA}=\frac{1}{2}\widehat{BOC}=\frac{1}{2}sđ\widehat{BC}\end{cases}}\)
\(\Rightarrow\widehat{ABH}=\widehat{BOA}\)
Xét tam giác ABH và tam giác AOB có:
\(\hept{\begin{cases}\widehat{BAO}chung\\\widehat{ABH}=\widehat{BOA}\left(cmt\right)\end{cases}\Rightarrow\Delta ABH~\Delta AOB\left(g-g\right)}\)
\(\Rightarrow\frac{AB}{AH}=\frac{AO}{AB}\)
\(\Rightarrow AB^2=AH.AO\left(1\right)\)
b) Xét tam giác ABD và tam giác AEB có:
\(\hept{\begin{cases}\widehat{BAE}chung\\\widehat{ABD}=\widehat{AEB}\left(=\frac{1}{2}sđ\widebat{BD}\right)\end{cases}\Rightarrow\Delta ABD~\Delta AEB\left(g-g\right)}\)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AB}\)
\(\Rightarrow AB^2=AD.AE\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AH.AO=AD.AE\)
\(\Rightarrow\frac{AH}{AD}=\frac{AE}{AO}\)
Xét tam giác ADH và tam giác AOE có:
\(\hept{\begin{cases}\widehat{OAE}chung\\\frac{AH}{AD}=\frac{AE}{AO}\end{cases}}\Rightarrow\Delta ADH~\Delta AOE\left(c-g-c\right)\)
\(\Rightarrow\widehat{AHD}=\widehat{AEO}\)
Xét tứ giác DHOE có \(\widehat{AHD}=\widehat{AEO}\)
\(\Rightarrow DHOE\)nội tiếp ( dhnb )
=> D,H,O,E thuộc một đường tròn (3)
Ta có: OK là đường trung trực của DE
Xét tam giác KDO và tam giác KEO có:
\(\hept{\begin{cases}KD=KE\\OD=OE\\OKchung\end{cases}\Rightarrow\Delta KDO=\Delta KEO\left(c-c-c\right)}\)
\(\Rightarrow\widehat{KDO}=\widehat{KEO}=90^0\)
Xét tứ giác KDOE có: \(\widehat{KDO}=\widehat{KEO}=90^0\)
Mà 2 góc này ở vị trí đối nhau của tứ giác KDOE
\(\Rightarrow KDOE\)nội tiếp
=> K,D,O,E thuộc đường tròn đường kính OK
Từ (3) và (4) => D,K,E,O,H thuộc đường tròn đường kính OK
c) Vì K,,O,H thuộc đường tròn đường kính OK
\(\Rightarrow\widehat{KHO}=90^0\)
\(\Rightarrow KH\perp HO\)
Mà \(BC\perp HO\)
\(\Rightarrow K,B,C\)thẳng hàng