Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A O B C E D K H I
a) Do H là trung điểm ED nên \(OH⊥DE\) .
Theo tính chất hai tiếp tuyến cắt nhau ta cũng có \(OK⊥DC\)
Vậy thì \(\Delta HOA\sim\Delta IKA\left(g-g\right)\Rightarrow\frac{OA}{OK}=\frac{AH}{AI}\Rightarrow AI.AO=AK.AH\)
b) Ta thấy \(AD.AE=AB^2=AI.AO=AK.AH\)
Vậy nên \(\frac{1}{AD}+\frac{1}{AE}=\frac{AD+AE}{AD.AE}=\frac{AD+AE}{AH.AK}=\frac{2AH}{AH.AK}=\frac{2}{AK}.\)

a) Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC
Xét ΔOBC có OB=OC(=R)
nên ΔOBC cân tại O(Định nghĩa tam giác cân)
mà OH là đường cao ứng với cạnh BC
nên H là trung điểm của BC(Đpcm)
sao không có câu B bạn ơi ?? có câu c càng tốt nhưng không làm được thì bỏ qua . nhưng bạn giúp minh câu B với , thankkk

Bài này căng đấy =))
C E B A D O I H
a) Do AB là tiếp tuyến của (O) với B là tiếp điểm (gt)
nên : \(AB\perp OB\)( tc tiếp tuyến )
\(\Rightarrow\widehat{ABO}=90^o\)(1)
Do H là trung điểm của dây DE (gt)
nên : \(OH\perp DE\)( liên hệ giữa đường kính và dây )
\(\Rightarrow\widehat{AHO}=90^o\)(2)
- Xét tứ giác ABOH ta có :
+) \(\widehat{ABO}\)và \(\widehat{AHO}\)là hai góc đối diện
+) \(\widehat{ABO}+\widehat{AHO}=90^o+90^o=190^o\)( do (1) và (2))
=> ABOH là tứ giác nội tiếp
=> 4 điểm A , B , O , H thuộc cùng 1 đường tròn ( đpcm )
b) Ta có : +) \(\widehat{B_1}\)là góc giữa tia tiếp tuyến và dây cung chắn cung \(\widehat{BD}\)của (O)
+) \(\widehat{E_1}\)là góc nội tiếp chắn cung \(\widehat{BD}\)của (O)
\(\Rightarrow\widehat{B_1}=\widehat{E_1}=\frac{1}{2}sđ\widebat{BD}\)( tính chất )
Xét 2 tam giác : ABD và AEB có :
\(\widehat{B_1}=\widehat{E_1}\left(cmt\right)\)
\(\widehat{A}\)chung
\(\Rightarrow\Delta ABD~\Delta AEB\left(g.g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{BD}{EB}\)( tỉ số đồng dạng )
\(\Rightarrow\frac{AB}{AE}=\frac{BD}{BE}\left(đpcm\right)\)
P/s : câu a) có nhiều cách chứng minh khác nữa bạn nhé . Bạn làm cách này có thể hay hơn là vì những gì đã nói ở trên về phương pháp trình bày và đồng thời chứng minh cũng áp dụng được cho nhiều bài khác ( Khi \(\widehat{ABO}\)và \(\widehat{AHO}\)không phải là những góc 90 độ )

Mình chưa vẽ hình nhưng mà câu c bạn có sai không? Tại vì bạn ghi thế thì có khác gì chứng minh AK=AD đâu. Bạn xem lại nhá
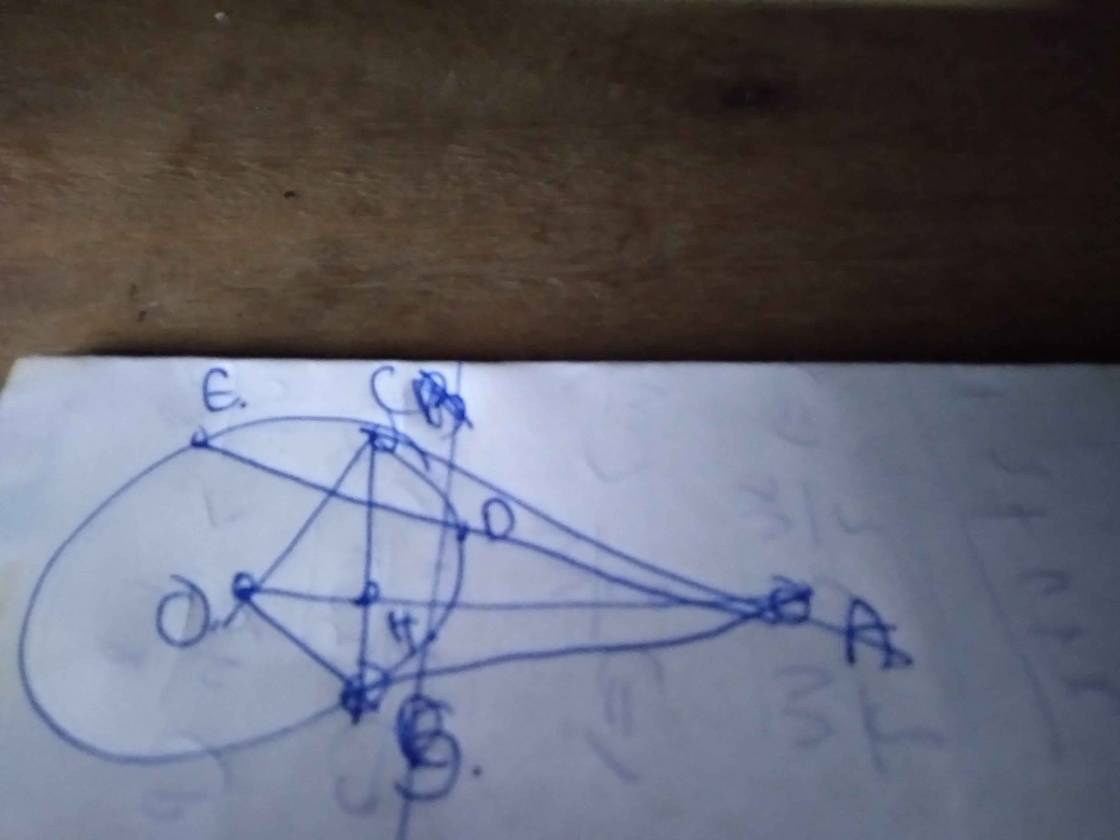
A B C D E K I O H
Bo de \(AD.AE=AC^2\) (ban tu chung minh nha , cu tam giac dong dang la ra )
xet \(AD+AE=AD+DH+AD+HE=AH+AD+DH=2AH\)
=> \(\frac{1}{AD}+\frac{1}{AE}=\frac{AD+AE}{AD.AE}=\frac{2AH}{AC^2}\) (1)
ta phai cm \(\frac{2AH}{AC^2}=\frac{2}{AK}\Leftrightarrow AH.AK=AC^2\) (2)
do H la trung diem DE => \(OH\perp DE=>\widehat{ABO}=\widehat{AHO}=\widehat{ACO}=90^0\)
=> A,B,O,H,C thuoc duong tron duong kinh AO
=> \(\widehat{AHC}=\widehat{ABC}\left(\frac{1}{2}sd\widebat{AC}\right)\)
ma \(\widehat{ABC}=\widehat{ACK}\) tinh chat 2 tiep tuyen cat nhau
=> \(\widehat{ACK}=\widehat{AHC}\) lai co \(\widehat{CAK}=\widehat{HAC}\)
=> \(\Delta AKC\approx\Delta ACH\left(g-g\right)\)
=> \(\frac{AK}{AC}=\frac{AC}{AH}\Leftrightarrow AK.AH=AC^2\) (3)
Tu (1),(2),(3) ta co dpcm