Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ thấy pt (AB): y=0 : trục hoành
Gọi H là chân đường vuông góc kẻ từ I đến AB, đặt IH=a
=> I(a;a) ( do (AB) là trục hoành và I thuộc đường thẳng x=y)
*Sử dụng công thức diện tích hình bình hành=> tính được IH => tọa độI ( hai trường hợp)
Vì I là trung điểm AC, BD => tọa độ C,D

Đáp án D
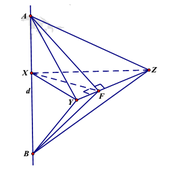
V A B Y Z = V A . X Y Z + V B . X Y Z = 1 3 A X . S X Y Z + 1 3 B X . S X Y Z = 1 3 S X Y Z A X + X B ≥ 1 3 S X Y Z .2 A X . X B
= 1 3 S X Y Z .2 X F ⇒ V A B Y Z nhỏ nhất ⇔ AX = X B .


- Tính khoảng cách từ B đến d theo t và tìm GTLN của khoảng cách.
- Tìm t và suy ra tọa độ của M.
Cách giải:
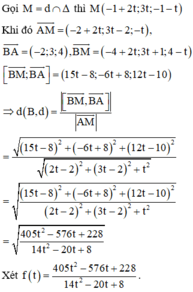
Sử dụng MTCT (chức năng TABLE với bước START nhập -5, bước END nhập 5 và bước STEP nhập 1 ta sẽ được kết quả GTLN f t = 29 tại t = 2)


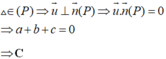
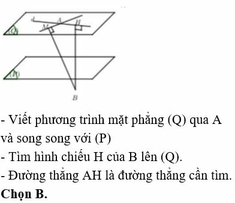

Nếu hai điểm A và B nằm về hai phía của đường thẳng d
\(\Rightarrow\)điểm C cần tìm là giao điểm của AB và d.
Bây giờ xét trường hợp A,B nằm về một phía của d. Lấy điểm A′ đối xứng với A qua d, ta có:AC+CB=A′C+CB
Mà A′C+CB ≥ A′B (dấu bằng xảy ra khi là giao điểm của A′B′ và d)
. Vậy trong trường hợp này CA + CB nhỏ nhất khi điểm C thỏa mãn bài toán là giao điểm của A′B và d
Đúng thì tích nha !
Gọi C là giao điểm của dường thẳng d và đoạn thẳng AB, C' là điểm bất kì nằm trên đường thẳng d ( C' # C ). Hãy chứng minh AC' + C'B > AC + CB để suy ra C là điểm phải tìm