Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B M C O O 1 2 O I E D N
a) Có ^AO1O2 = ^AO1M/2 = 1/2.Sđ(AM của (O1) = ^ABM = ^ABC. Tương tự ^AO2O1 = ^ACB
Suy ra \(\Delta\)AO1O2 ~ \(\Delta\)ABC (g.g) (đpcm).
b) Từ câu a ta có \(\Delta\)AO1O2 ~ \(\Delta\)ABC. Hai tam giác này có đường trung tuyến tương ứng AO,AI
Khi đó \(\Delta\)AOO1 ~ \(\Delta\)AIB (c.g.c) => \(\frac{AO}{AO_1}=\frac{AI}{AB}\). Đồng thời ^OAI = ^O1AB
=> \(\Delta\)AOI ~ \(\Delta\)AO1B (c.g.c). Mà \(\Delta\)AO1B cân tại O1 nên \(\Delta\)AOI cân tại O (đpcm).
c) Xét đường tròn (O1): ^DAM nội tiếp, ^DAM = 900 => DM là đường kính của (O1)
=> ^DBM = 900 => DB vuông góc với BC. Tương tự EC vuông góc với BC
Do vậy BD // MN // CE. Bằng hệ quả ĐL Thales, dễ suy ra \(\frac{ND}{NE}=\frac{MB}{MC}\)(1)
Áp dụng ĐL đường phân giác trong tam giác ta có \(\frac{MB}{MC}=\frac{AB}{AC}\)(2)
Từ (1) và (2) suy ra \(\frac{ND}{NE}=\frac{AB}{AC}\)=> ND.AC = NE.AB (đpcm).

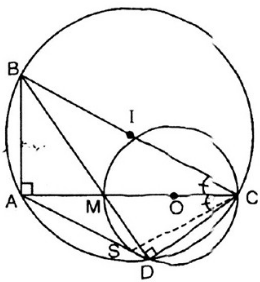
a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB