Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H K I D E
a) Tao có :) \(\Delta ABC\)cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
T lại có :) \(\widehat{ABC}=\widehat{HBD}\left(đđ\right)\)
\(\widehat{ACB}=\widehat{KCE}\left(đđ\right)\)
\(\Rightarrow\widehat{HBD}=\widehat{KCE}\)
Xét \(\Delta HBD\)và \(\Delta KCE\)t có :)
\(\widehat{HBD}=\widehat{KCE}\)
\(BD=CE\)
\(\widehat{DHB}=\widehat{EKC}\left(=90^o\right)\)
\(\Rightarrow\Delta HBD=\Delta KCE\left(ch-gn\right)\)
\(\Rightarrow HB=KC\left(đpcm\right)\)
b) T có :) \(\widehat{ABH}+\widehat{ABC}=180^o\)( kề bù )
\(\widehat{ACK}+\widehat{ACB}=180^o\)( kề bù )
Mà :) \(\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\widehat{ABH}=\widehat{ACK}\)
Xét \(\Delta AHB\)và \(\Delta AKC\)có :)
\(HB=CK\)
\(\widehat{ABH}=\widehat{ACK}\)
\(AB=AC\)
\(\Rightarrow\Delta AHB=\Delta AKC\left(c-g-c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AKC}\left(đpcm\right)\)
c) Do \(\Delta ABC\)cân tại A \(\Rightarrow\widehat{ABC}=\frac{180^o-\widehat{BAC}}{2}\left(1\right)\)
Mà :) \(AB=AC\)
\(BD=CE\)
\(\Rightarrow AB+BD=AC+CE\)
\(\Rightarrow AD=AE\)
\(\Rightarrow\Delta ADE\)cân tại A \(\Rightarrow\widehat{ADE}=\frac{180^o-\widehat{BAC}}{2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{ABC}=\widehat{ADE}\)
Mà hai góc trên đồng vị :)
\(\Rightarrow HK//DE\left(đpcm\right)\)
d) Theo câu b t có \(\Delta AHB=\Delta AKC\)
\(\Rightarrow\hept{\begin{cases}AH=AK\\\widehat{HAB}=\widehat{KAC}\end{cases}}\)
\(\Rightarrow\widehat{HAB}+\widehat{BAC}=\widehat{KAC}+\widehat{BAC}\)
\(\Leftrightarrow\widehat{HAC}=\widehat{KAB}\)
Xét \(\Delta AHE\)và \(\Delta AKD\)có :)
\(\widehat{HAC}=\widehat{KAB}\)
\(AH=AK\)
\(AE=AD\)
\(\Rightarrow\Delta AHE=\Delta AKD\left(c-g-c\right)\left(đpcm\right)\)
e) \(\Rightarrow\widehat{AHE}=\widehat{AKD}\)
\(\Leftrightarrow\widehat{AHK}+\widehat{KHE}=\widehat{AKH}+\widehat{HKD}\)
Mà :) \(\widehat{AHK}=\widehat{AKH}\)( câu b )
\(\Rightarrow\widehat{KHE}=\widehat{HKD}\Rightarrow\Delta HIK\)cân tại I
\(\Rightarrow HI=IK\)
Xét \(\Delta AHI\)và \(\Delta AKI\)có :)
\(HI=IK\)
\(AH=AK\)
Chung AI
\(\Rightarrow\Delta AHI=\Delta AKI\left(c-c-c\right)\)
\(\Rightarrow\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAB}+\widehat{BAI}=\widehat{CAI}+\widehat{KAC}\)
Lại có :) \(\widehat{HAB}=\widehat{KAC}\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\)
\(\Rightarrow\)AI là tia phân giác \(\widehat{BAC}\)hay \(\widehat{DAE}\)
Mà \(\Delta DAE\)cân tại A
\(\Rightarrow AI\perp DE\)( do đường phân giác của đỉnh tam giác cân cũng chính là đường cao của tam giác cân đó )
Vậy .... :)
Hình vẽ : 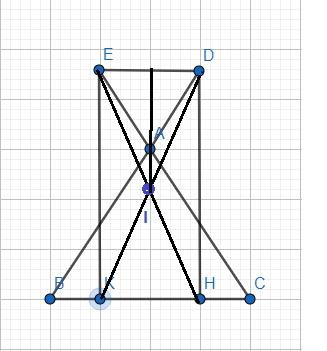
a) Dễ nhận thấy DE = KH = 1/2 BC
Do đó KH = 1/2BC suy ra KB + CH = 1/2BC=KH
Vậy KB + CH = KH
Do vậy 2KB + CH = KH + KB (1)
KB + 2CH = KH + KB (2)
Từ đó suy ra CH = KB
Mà HB = KH + KB (3)
CK = KH + HC (4)
Mà KB = HC nên KH + KB = KH + HC hay HB = CK
b) Chứng minh \(\Delta AHB=\Delta AKC\)
Ta có: \(\Delta AHB=\Delta AKC\left(c.g.c\right)\)
Suy ra \(\widehat{AHB}=\widehat{AKC}\)
c) Theo hình vẽ ta có BD = CE và BD là tia đối của BA, nên BD thẳng hàng với BA
CE là tia đối của CA nên CE thẳng hàng với CA
Do đó CE = BD . DO đó EK = DH.
Theo đề bài DH và EK cùng vuông góc BC (5) mà DH = EK do đó \(\widehat{D}=90^o;\widehat{E}=90^o\)(6)
Từ (5) và (6) suy ra HK song song DE
Sau đó tự làm tiếp

a) ta có: tam giác ABC cân tại A
=> góc ABC = góc ACB ( tính chất tam giác cân)
mà góc ABC = góc HBD; góc ACB = góc KCE ( đối đỉnh)
=> góc HBD = góc KCE (= góc ABC = góc ACB)
Xét tam giác DHB vuông tại H và tam giác EKC vuông tại K
có: DB = EC (gt)
góc HBD = góc KCE (cmt)
\(\Rightarrow\Delta DHB=\Delta EKC\left(ch-gn\right)\)
=> HB = KC ( 2 cạnh tương ứng)
b) ta có: góc ABC + góc ABH = 180 độ ( kề bù)
góc ACB + góc ACK = 180 độ ( kề bù)
=> góc ABC + góc ABH = góc ACB + góc ACK ( = 180 độ)
=> góc ABH = góc ACK ( góc ABC = góc ACB)
Xét tam giác ABH và tam giác ACK
có: AB = AC (gt)
góc ABH = góc ACK
BH = CK (phần a)
\(\Rightarrow\Delta ABH=\Delta ACK\left(c-g-c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AKC}\) ( 2 góc tương ứng)
c) ( Nối H với E)
ta có: \(DH\perp BC⋮H\)
\(EK\perp BC⋮K\)
\(\Rightarrow DH//EK\) ( định lí từ vuông góc đến //)
=> góc DHE = góc KEH ( so le trong)
ta có: tam giác DHB = tam giác EKC ( phần a)
=> DH = EK ( 2 cạnh tương ứng)
Xét tam giác DHE và tam giác KEH
có: DH = KE ( cmt)
góc DHE = góc KEH (cmt)
HE là cạnh chung
\(\Rightarrow\Delta DHE=\Delta KEH\left(c-g-c\right)\)
\(\Rightarrow\widehat{DEH}=\widehat{KHE}\) ( 2 góc tương ứng)
mà góc DEH và góc KHE nằm ở vị trí so le trong
=> HK // DE ( định lí //)
d) ta có: \(\Delta ABH=\Delta ACK\) ( phần b)
=> AH = AK ( 2 cạnh tương ứng)
góc BAH = góc CAK ( 2 góc tương ứng)
=> góc BAH + góc BAC = góc CAK + góc BAC
=> góc HAE = góc KAD
ta có: AB = AC; BD = CE
=> AB + BD = AC + CE
=> AD = AE
Xét tam giác AHE và tam giác AKD
có: AE = AD (cmt)
góc HAE = góc KAD (cmt)
AH = AK ( cmt)
\(\Rightarrow\Delta AHE=\Delta AKD\left(c-g-c\right)\)

a,Ta có: góc HBD=góc ABC
góc KCE = góc ACB
Mà góc ABC = góc ACB ( tam giác ABC cân)
Xét tam giác BDH và tam giác CEK:
Góc DHB = góc EKC
BD=CE (GT)
Góc HBD = góc KCE (cmt)
=> tam giác BDH = tam giác CEK ( cạnh huyền - góc nhọn )
b, Ta có: AB=AC;BD=CE
=> AB+BD=AC+CE
<=>AD=AE
Xét tam giác AHD và tam giác AKE:
HD=KE(tam giác BDH = tam giác CEK)
Góc HDB=góc KEC(tam giác BDH = tam giác CEK)
AD=AE(cmt)
=> tam giác AHD = tam giác AKE
=>AH=AK và góc HAD = góc KAE
Xét tam giác AHB và tam giác AKC
AH=AK(cmt)
góc HAB = góc KAC(cmt)
AB=AC( tam giác ABC cân)
=> tam giác AHB = tam giác AKC
=> Góc AHB = góc AKC

ta có: góc ABC = góc HBD (đối đỉnh ) ; góc ACB = góc KCE (đối đỉnh) ; góc ABC = góc ACK( \(\Delta\)ABC)
=> góc HBD = góc KCE
Mà DH vuông góc BC => góc BHD =90 độ ; EK vuông góc BC => góc CKE =90 độ
a) Xét tam giác vuông BHD và tam giác vuông CKE có :
BD = CE (gt)
góc HBD = góc KCE
=> \(\Delta\)BHD = \(\Delta\)CKE ( cạnh huyền - góc kề)
=> HB=KC (c/c/t/u)
góc HBD = góc KCE (cmt)
góc HBD + góc HBA= 180 độ ; góc KCE + góc ACK = 180 độ
=> góc ABH = góc ACK
xét tam giác ABH và tam giác ACK có :
HB=KC (cmt
góc ABH = góc ACK
AB=AC (\(\Delta\)ABC can )
xét tam giác ABH = tam giác ACK (c.g.c)
=> góc AHB = góc AKC (c/g/t/u)

A B C H K D E I
a, \(\Delta ABC\)cân tại A = > \(\widehat{ABC}=\widehat{ACB}\)
Xét \(\Delta HBD\perp H\)và \(\Delta KCE\perp K\)có :
\(BD=CE\left(gt\right)\)
Mặt khác : góc HBD đối đỉnh với góc ABC = > góc HBD = góc ABC
góc KCE đối đỉnh với góc ACB = > góc KCE = góc ACB
Mà góc ABC = ACB = > góc HBD = góc KCE
\(=>\Delta HBD=\Delta KCE\left(ch-gn\right)\)
= > HB = CK ( 2 cạnh tương ứng )
b, Xét \(\Delta AHB\)và \(\Delta AKC\)có
HB = CK ( cmt )
AB = AC ( gt )
\(\widehat{HBD}+\widehat{HBA}=180^0\)
= > \(\widehat{HBA}=180^0-\widehat{HBD}\)( 1 )
\(\widehat{KCE}+\widehat{KCA}=180^0\)
= > \(\widehat{KCA}=180^0-\widehat{KCE}\)( 2 )
Từ ( 1 ) và ( 2 ) = > \(\widehat{HBA}=\widehat{KCA}\)
\(=>\Delta AHB=\Delta AKC\left(c.g.c\right)\)
c, \(\Delta ABC\)cân tại A = > \(\widehat{ABC}=\frac{180^0-\widehat{BAC}}{2}\)( 1 )
\(B\in AD\)
= > AB + BD = AD ( * )
\(C\in AE\)
= > AC + CE = AE ( ** )
Từ ( * ) và ( ** ) = > AD = AE hay \(\Delta ADE\)cân tại A
= > \(\widehat{ADE}=\frac{180^0-\widehat{EAD}}{2}\)( 2 )
Từ ( 1 ) và ( 2 ) = > \(\widehat{ABC}=\widehat{ADE}\)hay HK // DE
d, Xét \(\Delta AHE\)và \(\Delta AKD\)có:
\(\widehat{A}\)chung
AH = AK ( cmt )
AE = AD ( cmt )
= > \(\Delta AHE=\Delta AKD\left(c.g.c\right)\)
câu e, bạn làm nốt nhé

a/ Ta có: góc HBD đối đỉnh góc ABC; góc KCE đối đỉnh góc ACB mà ABC=ACB( Tg ABC cân tại A) => Góc HBD = góc KCE.
Xét tg HBD ( vuông tại H) và tg KCE ( vuông tại K) có:
góc HBD = góc KCE ( cmt)
DB=CE (gt)
=> Tg HBD=Tg KCE( ch-gn)
=> HB=CK( hai cạnh tương ứng)
b/ Xét tg AHB và tg AKC có:
HB=CK ( cmt)
góc ABH= góc ACK ( cùng kề bù với hai góc bằng nhau)
AB=AC( tg ABC cân tại A)
=> tg AHB= tg AKC ( c.g.c)
=> góc AHB = góc AKD( hai góc tương ứng)
c/ Ta có : AB+BD=AD; AC+CE=AE mà AB=AC và BD=CE => AD=AE
Trong tg ADE có AD=AE => Tg ADE cân tại A
Ta có: góc ABC= góc ACB =\(\frac{180^0-gócBAC}{2}\)và góc ADE= góc AED=\(\frac{180^0-gócBAC}{2}\)
=> góc ABC=góc ACB= góc ADE= góc AED .
Mà ABC và ADE cùng nằm ở vị trí đồng vị => HK//DE
d/ ta có: góc HAB+ góc BAC= góc HAC
góc KAC+ góc BAC= góc KAB
mà góc HAB=góc CAK ( tg AHB= tg AKC) => góc HAC= góc KAB.
Xét tg AHE và tg AKD có:
AH = AK( tg AHB= tg AKC)
góc HAC= góc KAB ( CMT)
AE=AD
=> Tg AHE =tg AKD ( c.g.c)
e/ Mk` chưa giải được.
mấy câu a,b,c,d chắc bạn biết làm hết rồi nên mình giải câu e nha
cmd tam gi1c ahi=aki(c.c.c)suy ra góc hai=kai
cmđ dai=eai
gọi giao điểm của ai va bc la kcòn với de là n
cmd tam giac bak=cak suy ra gó akb=akc =90 độ
tương tự cmd and =90 độ
vậy ai vuông góc với de
mình bận nên ghi hơi tat nên chổ nào bạn ko hiểu ở bài này có the hoi mình ,nếu bnko hieu caub,c,d có thể hỏi mình
mấy câu a,b,c,d chắc bạn biết làm hết rồi nên mình giải câu e nha
cmd tam gi1c ahi=aki(c.c.c)suy ra góc hai=kai
cmđ dai=eai
gọi giao điểm của ai va bc la kcòn với de là n
cmd tam giac bak=cak suy ra gó akb=akc =90 độ
tương tự cmd and =90 độ
vậy ai vuông góc với de
chúc bn hok tốt @_@