Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1 a,Ta có ∆ ABC= ∆ HIK, nên cạnh tương ứng với BC là cạnh IK
góc tương ứng với góc H là góc A.
ta có : ∆ ABC= ∆ HIK
Suy ra: AB=HI, AC=HK, BC=IK.
=
,
=
,
=
.
b,
∆ ABC= ∆HIK
Suy ra: AB=HI=2cm, BC=IK=6cm, =
=400
2.
Ta có ∆ABC= ∆ DEF
Suy ra: AB=DE=4cm, BC=EF=6cm, DF=AC=5cm.
Chu vi của tam giác ABC bằng: AB+BC+AC= 4+5+6=15 (cm)
Chu vi của tam giác DEF bằng: DE+EF+DF= 4+5+6=15 (cm

Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
Giải:
Xem hình vẽ
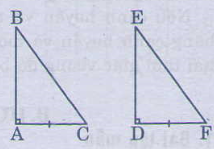
* Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)

a) Cạnh tương ứng với AC là HK
Góc tương ứng với góc I là góc B
b) Các cạnh bằng nhau: AB = HI ; BC = IK; AC = HK
Các góc bằng nhau: góc A = góc H; góc B = góc I; góc C = góc K
xét \(\Delta ABC\) và \(\Delta HIK\)
a) cạnh tương ứng với cạnh \(AC\)là \(HK\)
góc tương ứng với góc \(I\)là góc \(B\)
b) các cạnh = nhau: \(AB=HI\); \(AC=HK\); \(BC=IK\)
các góc = nhau \(\widehat{A}=\widehat{H}\); \(\widehat{B}=\widehat{I}\); \(\widehat{C}=\widehat{K}\)

a) Vì \(\Delta ABC=\Delta HIK\)
nên BC = IK (2 cạnh t/ư)
và \(\widehat{A}=\widehat{H}\) (2 góc t/ư)
b) Do \(\Delta ABC=\Delta HIK\)
=> AB = HI; AC = HK (2 cạnh t.ư); BC = IK (câu a)
và \(\widehat{A}=\widehat{H}\) (câu a); \(\widehat{B}=\widehat{I}\) và \(\widehat{C}=\widehat{K}\) (2 góc t/ư).

các cạnh bằng nhau là
AB=DE
BC=EF
AC=DF
các góc bằng nhau là
góc ABC= góc DEF
góc BAC= góc EDF
góc ACB= góc DFE

a: ΔABC và ΔEFD
Để ΔABC=ΔEFD theo trường hợp c-g-c thì BC=FD
b: ΔABC=ΔEFD
nên AB=EF=5cm; AC=ED=6cm; BC=FD=6cm
=>\(C_{ABC}=C_{EFD}=5+6+6=17\left(cm\right)\)

1/ Ta có: tam giác ABC = tam giác DEF
=> góc A = góc D
góc B = góc E
góc C = góc F
Ta có: góc A + góc B + góc C = 1800
1300 + góc C = 1800
góc C = 1800-1300 = 500
Ta có: góc A + góc B = 1300
góc A + 550 = 1300
góc A = 1300 - 550 =750
Vậy góc A = góc D = 750
góc B = góc E = 550
góc C = góc F = 500
2/ Ta có: tam giác DEF = tam giác MNP
=> DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10 cm
Mà NP - MP = EF - FD = 2 cm
EF = (10 + 2) : 2 = 6 (cm)
FD = (10 - 2) : 2 = 4 (cm)
Vậy DE = MN = 3 cm
EF = NP = 6 cm
FD = MP = 4 cm
1) Ta có: ( \(\widehat{A}\) + \(\widehat{B}\)) + \(\widehat{C}\) = 180o
hay 130o + \(\widehat{C}\) = 180o
\(\Rightarrow\) \(\widehat{C}\) = 180o - 130o = 50o
Vì ΔABC = ΔDEF nên ta có:
\(\widehat{C}\) = \(\widehat{F}\) = 50o
\(\widehat{E}\) = \(\widehat{B}\) = 55o
Ta có: \(\widehat{A}\) + \(\widehat{B}\) = 130o hay \(\widehat{A}\) + 55o = 130o
\(\Rightarrow\) \(\widehat{A}\) = 130o - 55o = 75o
\(\Leftrightarrow\) \(\widehat{A}\) = \(\widehat{D}\) = 75o
Vậy: \(\widehat{A}\) = \(\widehat{D}\) = 75o
\(\widehat{B}\) = \(\widehat{E}\) = 55o
\(\widehat{C}\) = \(\widehat{F}\) = 50o
2) ΔDEF = ΔMNP nên:
\(\Rightarrow\) DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10cm
mà ΔDEF = ΔMNP
\(\Rightarrow\) NP - MP = EF - FD = 2cm
\(\Rightarrow\) EF = \(\frac{10+2}{2}\) = 6cm
FD = 6cm - 2cm = 4cm
Vậy: DE= MN = 3cm
EF = NP = 6cm
FD = PM = 4cm
\(\Delta ABC=\Delta DEF\Rightarrow\widehat{A}=\widehat{D},\widehat{B}=\widehat{E},\widehat{C}=\widehat{F},AB=DE,AC=DF,BC=EF\)
Ta có: ∆ABC = ∆DEF
Suy ra: AB = DE; AC = DF; BC = EF
∠A = ∠D ; ∠B = ∠E ; ∠C = ∠F