Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

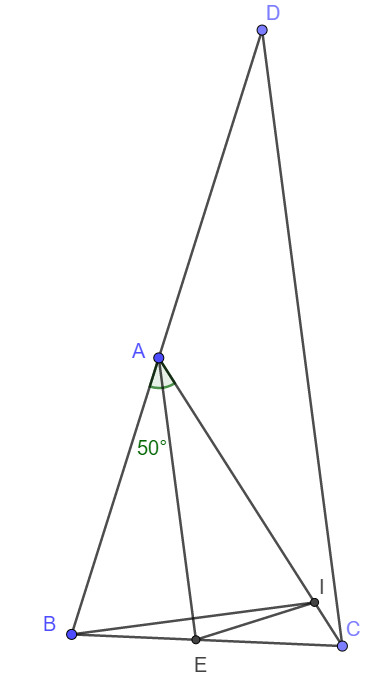
a) Xét tam giác ABE và tam giác AIE có:
Cạnh AE chung
AB = AI
\(\widehat{BAE}=\widehat{IAE}\)
\(\Rightarrow\Delta ABE=\Delta AIE\left(g-c-g\right)\)
\(\Rightarrow EB=EI\) (Hai cạnh tương ứng)
b) Xét tam giác ABI cân tại A nên có tia phân giác AE đồng thời là đường cao. Vậy nên \(AE\perp BI\)
Lại có AE // DC nên \(BI\perp CD.\)

a/ tgiác ACD và tgiác AME là hai tgiác vuông tại A.
AD = AE (gt)
góc(ADC) = góc (AEM) (góc có cạnh tương ứng vuông góc)
=> tgiácACD = tgiácAME (g.c.g)
b/ ta có: AG//EH (cùng vuông góc với CD)
=> AG // IH
mà gt => AI // GH
vậy AGHI là hình bình hành
=>AG = IH.
mặt khác theo cm trên ta có: tgiác ACD = tgiác AME
=> AM = AC = AB
=> A là trung điểm BM, mà AI // BC
=> AI là đường trung bình của tgiác MBH
=> I là trung điểm của MH.
vậy: IM = IH = AG
có: AM = AB
góc BAG = góc AMI (so le trong)
=> tgiác AGB = tgiác MIA ( c.g.c)
c/ có AG//MH, A là trung điểm BM
=> AG là đường trung bình của tgiácBMH
=> G là trung điểm BH
hay BG = GH.

a, xét tam giác ABE và tam giác ACD có:
AC=AB(gt)
góc A chung
góc ABE = góc ACD( do ABC= góc ACB, tia p/giác)
suy ra tam giác ABE= tam giác ACD(g.c.g)
suy ra BE=CD, AE=AD(đpcm)
E A B C I D 2 1