Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C N D O X X K I X X X X
Đề bài bạn phải ghi là trên tia đối của tia AK lấy điểm I sao cho AI = AK.
a) Xét \(\Delta ABC\)có:
NA = NC (giả thiết)
DB = DC (giả thiết)
\(\Rightarrow\)ND là đường trung bình của \(\Delta ABC\)
\(\Rightarrow ND//AB\)(tính chất) (1)
Mà \(AB\perp AC\)(vì \(\Delta ABC\)vuông tại A)
\(\Rightarrow AB\perp AN\) (2)
Do đó \(ND\perp AN\)(3)
Xét tứ giác ANDB có (1), (2), (3).
\(\Rightarrow\)ANDB là hình thang vuông (điều phải chứng minh)

Lời giải:
Từ $B$ kẻ \(BT\parallel AC\)
Xét tam giác $DAK$ có \(BT\parallel AK\Rightarrow \) áp dụng định lý Thales:
\(\frac{BT}{AK}=\frac{BD}{DA}=\frac{1}{2}\Rightarrow AK=2BT(1)\) (do \(B\) là trung điểm của $AD$ )
Xét tam giác $BTM$ và $CKM$ có:
\(\left\{\begin{matrix} \angle TBM=\angle KCM(\text{so le trong})\\ \angle BMT=\angle CMK(\text{góc đối})\\ BM=MC\end{matrix}\right.\)
\(\Rightarrow \triangle BTM=\triangle CKM(g.c.g)\Rightarrow BT=CK(2)\)
Từ \((1),(2)\Rightarrow AK=2KC\) (đpcm).

Qua B kẻ BH // AC , cắt DM tại H
Ta có {BH // AK ; AB = BD => BH là đường trung bình của tam giác ADK
=> AK=2BH (1)
Dễ dàng chứng minh được tam giác MKC = tam giác MBH (g.c.g)
=> BH = CK (2)
Từ (1) và (2) suy ra AK = 2CK
Qua B Kẻ BH // AC , cắt DM tại H
Ta có : BH // AK
AB // BD
=> BH là đường trung bình của tam giác ADK
=> AK = 2 BH (1)
· * Xét tam giác MKC và tam giác MBH .
CÓ : BM = CM ( M là trung điểm của BC)
Góc M1= Góc M2 ( 2 góc đối đỉnh)
Góc MKC = MBH ( = 90 *)* là độ
=> Tam giác MKC = Tam giác MBH ( g. c . g)
=> BH = KC ( 2 cạnh tương ứng )(2)
Từ (1), (2) suy ra được AK = 2 KC

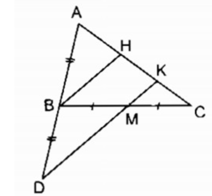
Gọi H là trung điểm của AK
Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.
⇒ BH // DK (tính chất đường trung bình của tam giác)
Hay BH // MK
Trong ∆ BCH ta có M là trung điểm của BC
MK // BH
⇒ CK = HK
AK = AH + HK = 2HK
Suy ra: AK = 2 KC ( vì HK =KC)