K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
1 tháng 1 2020
Bạn tham khảo lời giải tại đây:
Câu hỏi của Not Perfect - Toán lớp 8 | Học trực tuyến

22 tháng 4 2017
Giải:
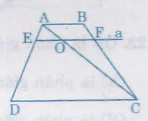
a) Nối AC cắt EF tại O
∆ADC có EO // DC => AEEDAEED = AOOCAOOC (1)
∆ABC có OF // AB => AOOCAOOC = BFFCBFFC (2)
Từ 1 và 2 => AEEDAEED = BFFCBFFC
b) Từ AEEDAEED = BFFCBFFC => AEED+AEAEED+AE= BFFC+BFBFFC+BF
Lời giải:
a)
Sử dụng công thức về tia phân giác ta có:
\(\frac{DI}{AI}=\frac{BD}{AB}\Rightarrow \frac{DI}{DA}=\frac{BD}{AB+BD}(1)\)
\(\frac{BD}{DC}=\frac{AB}{AC}\Rightarrow \frac{BD}{BC}=\frac{AB}{AB+AC}\Rightarrow BD=\frac{AB.BC}{AB+AC}(2)\)
Từ \((1);(2)\Rightarrow \frac{DI}{DA}=\frac{\frac{AB.BC}{AB+AC}}{AB+\frac{AB.BC}{AB+AC}}=\frac{AB.BC}{AB(AB+BC+AC)}=\frac{BC}{AB+BC+AC}=\frac{a}{a+b+c}\)
Ta có đpcm.
b)
Sử dụng kết quả phần a:
\(\frac{DI}{DA}=\frac{a}{a+b+c}\)
Bằng cách chứng minh hoàn toàn tương tự ta cũng có:
\(\frac{EI}{EB}=\frac{b}{a+b+c}; \frac{FI}{FC}=\frac{c}{a+b+c}\)
Do đó:
\(\frac{DI}{DA}+\frac{EI}{EB}+\frac{FI}{FC}=\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=1\)
Ta có đpcm.
Hình vẽ: