Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

A B C I H K F E a) Theo gt ta có :
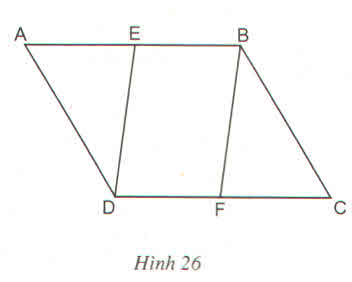
FD // AC => FD // AE ( E \(\in AC\)) ( 1)
DE // AB => DE // AF ( F \(\in AB\) ) (2)
từ (1)(2) \(\Rightarrow AEDF\) là hình bình hành ( theo dấu hiệu nhận biết hình bình 1)
b)
theo a) tao có AEDF là hình bình hành
hình bình hành có 2 đường chéo AD và EF giao nhau tại I
=> I là trung điểm của 2 đường chéo AD và EF ( t/c hình bình hành )
=> \(IF=IE\) hay F đối xứng với E qua I
a)Xét tứ giác AEDF có: DE//AB, DF//AC
\(\Rightarrow\)AEDE là hình bình hành
b) Vì 2 đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường nên IA=ID, IF=IE suy ra E đối xứng với F qua I

a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC

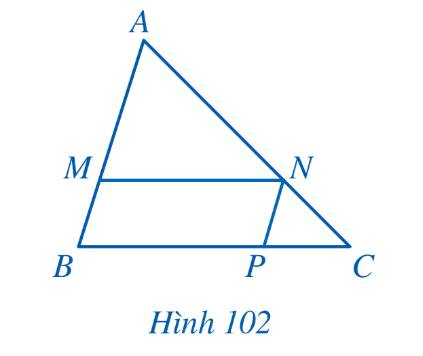
Vì BMNP là hình bình hành nên \(NP\parallel AB\)\(,\,\,MN = BP,\,\,BM = PN\)
\( \Rightarrow \frac{{NP}}{{AB}} = \frac{{CP}}{{CB}}\) (Định lý Thales)
Ta có: \(\frac{{MN}}{{BC}} = \frac{{BP}}{{BC}}\)
Khi đó: \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = \frac{{BP}}{{BC}} + \frac{{CP}}{{BC}} = \frac{{BC}}{{BC}} = 1\) (đpcm)

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật

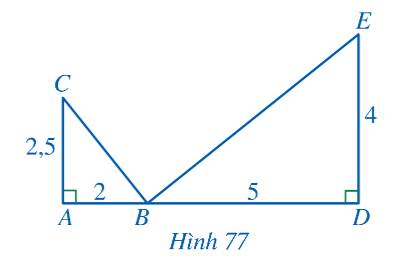
a) Ta thấy \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{AC}}{{DB}} = \frac{2,5}{5} = \frac{1}{2}\)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\)
Xét tam giác ABC và tam giác DEB có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\) và \(\widehat {CAB} = \widehat {BDE} = 90^\circ \)
\( \Rightarrow \Delta ABC \backsim \Delta DEB\) (c-g-c)
\( \Rightarrow \widehat {ABC} = \widehat {BED}\)
b) Vì \(\Delta ABC \backsim \Delta DEB\) nên \(\widehat {ACB} = \widehat {DBE}\)
Mà tam giác ABC vuông tại A nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \) hay \(\widehat {DBE} + \widehat {ABC} = 90^\circ \)
Ta thấy
\(\begin{array}{l}\widehat {DBE} + \widehat {CBE} + \widehat {ABC} = 180^\circ \\ \Rightarrow \widehat {CBE} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {CBE} = 90^\circ \end{array}\)
Vậy \(BC \bot BE\).
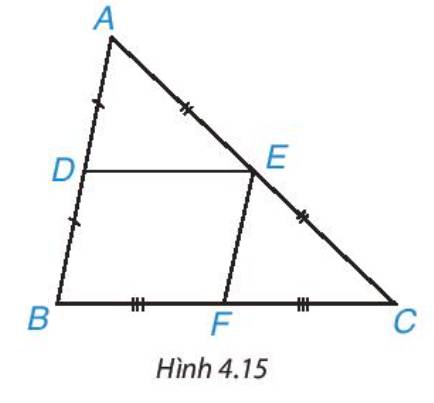
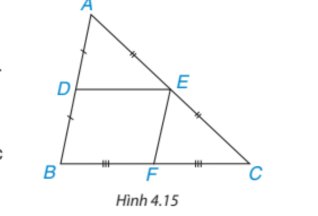

Chứng minh tương tự HĐ1, ta có EF // AB.
Xét tam giác DEFB có DE // BF, EF // BD
=> DEFB là hình bình hành.
=> DE = BF (hai cạnh tương ứng)
Mà F là trung điểm của BC => BF = \(\frac{1}{2}\)BC
=> DE = \(\frac{1}{2}\)BC