PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
9 tháng 4 2017
a) Dãy số bị chặn dưới vì un = 2n2 -1 ≥ 1 với mọi n ε N* và không bị chặn trên vì với số M dương lớn bất kì, ta có 2n2 -1 > M <=> n >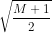 
.
tức là luôn tồn tại n ≥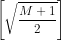 
+ 1 để 2
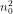- 1 > M.
b) Dễ thấy un > 0 với mọi n ε N*
Mặt khác, vì n ≥ 1 nên n2 ≥ 1 và 2n ≥ 2.
Do đó n(n + 2) = n2 + 2n ≥ 3, suy ra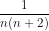 
.
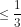Vậy dãy số bị chặn 0 < un 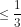với mọi n ε N*
c) Vì n ≥ 1 nên 2n2 - 1 > 0, suy ra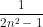 
> 0
Mặt khác n2 ≥ 1 nên 2n2 ≥ 2 hay 2n2 - 1≥ 1, suy ra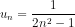 
≤ 1.
Vậy 0 < un ≤ 1, với mọi n ε N* , tức dãy số bị chặn.
d) Ta có: sinn + cosn = √2sin(n +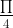 
), với mọi n. Do đó:
-√2 ≤ sinn + cosn ≤ √2 với mọi n ε N*
Vậy -√2 < un < √2, với mọi n ε N* .
BT
24 tháng 5 2017
TenAnh1 TenAnh1 A = (-4.36, -5.2) A = (-4.36, -5.2) A = (-4.36, -5.2) B = (11, -5.2) B = (11, -5.2) B = (11, -5.2)
Ta có :
u n + 1 − u n = − n + 1 2 + n + 1 + 1 − − n 2 + n + 1 = − n 2 − 2 n − 1 + n + 2 + n 2 − n − 1 = − 2 n < 0 ∀ n ≥ 1
Do đó ( u n ) là một dãy giảm.
Chọn đáp án D