Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo giả thiết \(\tan A,\tan B,\tan C\) lập thành cấp số cộng thì ta có : \(\tan A+\tan C=2\tan B\)
\(\Leftrightarrow\tan A+\tan C=\frac{\sin\left(A+C\right)}{\cos A.\cos C}=\frac{\sin B}{\cos A.\cos C}\Rightarrow\frac{2\sin B}{\cos B}=\frac{\sin B}{\cos A.\cos C}\)
\(\Leftrightarrow\frac{2}{\cos B}=\frac{1}{\cos A.\cos C}\Leftrightarrow2\cos A.\cos C=\cos B\)
\(\Leftrightarrow\cos\left(A+C\right)+\cos\left(A-C\right)=\cos B\)
\(\Leftrightarrow-\cos B+\cos\left(A-C\right)=\cos B\Leftrightarrow\cos B=\frac{1}{2}\cos\left(A-C\right)\le\frac{1}{2}\left(2\right)\)
( Vì \(0 <\)\(\cos\left(A-C\right)\le1\) )
Do 0 < B \(\le\pi\Rightarrow\) giá trị nhỏ nhất của \(B=\frac{\pi}{3}\)
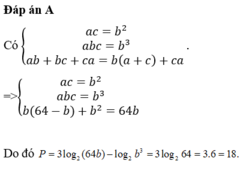
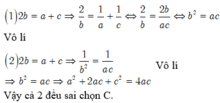

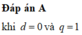
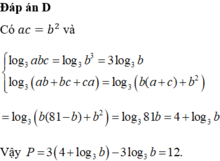

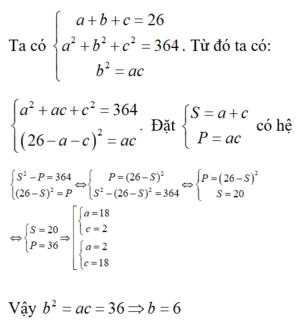

Đáp án B
Từ giả thiết ta có
b 2 = a c a + c = 2 ( b + 8 ) b + 8 2 = a ( c + 64 ) ⇔ b 2 = a c a + c = 2 ( b + 8 ) b + 8 2 = b 2 + 64 a ⇔ b 2 = a c c = 7 a + 8 b = 4 a − 4
⇔ 4 a - 4 2 = a 7 a + 8 c = 7 a + 8 b = 4 a - 4 ⇔ 9 a 2 - 40 a + 16 = 0 c = 7 a + 8 b = 4 a - 4 ⇔ a = 4 ; b = 12 ; c = 36 a = 4 9 ; b = - 20 9 ; c = 100 9
Do a,b,c tạo thành một dãy số tăng nên a = 4 ; b = 12 ; c = 36 .
Suy ra
a − b + 2 c = 4 − 12 + 2.36 = 64.