Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left\{{}\begin{matrix}u_1=1\\\frac{u_n}{n}=\frac{u_{n-1}}{n-1}+1\end{matrix}\right.\)
Đặt \(v_n=\frac{u_n}{n}\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_n=v_{n-1}+1\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSC với công sai \(d=1\)
\(\Rightarrow v_n=1+\left(n-1\right).1=n\)
\(\Rightarrow\frac{u_n}{n}=n\Rightarrow u_n=n^2\)
Câu b có vẻ đề sai, số hạng cuối không thể là \(u_n\) mà phải là 1 số hữu hạn ví dụ \(u_{2016}\) gì đó
Hoặc nếu nó là \(u_n\) thì đề sẽ là "tìm n lớn nhất sao cho..."
Dù sao từ tổng: \(\sum u_n=\sum n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}\) có thể dễ dàng giải được khi đề bài chính xác

\(u_3=u_2^2-u_2+2=4\)
\(S_1=1=\left(2-1\right)^2=\left(u_2-1\right)^2\)
\(S_2=2.5-1=9=\left(4-1\right)^2=\left(u_3-1\right)^2\)
Dự đoán \(S_n=\left(u_{n+1}-1\right)^2\)
Ta sẽ chứng minh bằng quy nạp:
- Với \(n=1;2\) đúng (đã kiểm chứng bên trên với \(S_1;S_2\))
- Giả sử đẳng thức đúng với \(n=k\)
Hay \(S_k=\left(u_1^2+1\right)\left(u_2^2+1\right)...\left(u_k^2+1\right)-1=\left(u_{k+1}-1\right)^2\)
Ta cần chứng minh:
\(S_{k+1}=\left(u_1^2+1\right)\left(u_2^2+1\right)...\left(u_k^2+1\right)\left(u_{k+1}^2+1\right)-1=\left(u_{k+2}-1\right)^2\)
Thật vậy:
\(S_{k+1}=\left[\left(u_{k+1}-1\right)^2+1\right]\left(u_{k+1}^2+1\right)-1\)
\(=\left(u_{k+1}^2-2u_{k+1}+2\right)\left(u_{k+1}^2+1\right)-1\)
\(=\left(u_{k+2}-u_{k+1}\right)\left(u_{k+2}+u_{k+1}-1\right)-1\)
\(=u_{k+2}^2-u_{k+2}-u_{k+1}^2+u_{k+1}-1\)
\(=u_{k+2}^2-u_{k+2}+2-u_{k+2}-1\)
\(=\left(u_{k+2}-1\right)^2\) (đpcm)

ta có : \(u_n=\frac{1+2^m}{2^m}\Rightarrow lim\left(u_n\right)=lim\left(\frac{1+2^m}{2^m}\right)=lim\left(1+\frac{1}{2^m}\right)=1\)

\(u_n=\frac{n+1}{n-1}u_{n-1}\)
\(u_{n-1}=\frac{n-1+1}{n-1-1}u_{n-2}=\frac{n}{n-2}u_{n-2}\)
\(u_{n-2}=\frac{n-1}{n-3}u_{n-3}\)
...
\(u_2=\frac{2+1}{2-1}u_1\)
Nhân vế với vế:
\(u_nu_{n-1}u_{n-2}...u_2=\frac{\left(n+1\right)n\left(n-1\right)...3}{\left(n-1\right)\left(n-2\right)\left(n-3\right)...1}u_{n-1}u_{n-2}u_{n-3}...u_1\)
\(\Leftrightarrow u_n=\frac{n\left(n+1\right)}{2}u_1=n\left(n+1\right)\)
\(u_n< 100\Rightarrow n^2+n< 100\)
\(\Leftrightarrow n^2+n-100< 0\Rightarrow n\le9\Rightarrow n=\left\{1;2;...;9\right\}\)
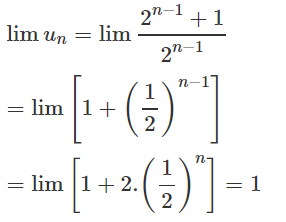
1) Có \(u_{n+1}-u_n=\dfrac{1}{2}u^2_n-2u_n+2=\dfrac{1}{2}\left(u_n-2\right)^2\) (1)
+) CM \(u_n>2\) (n thuộc N*)
n=1 : u1= 5/2 > 2 (đúng)
Giả sử n=k, uk > 2 (k thuộc N*)
Ta cần CM n = k + 1. Thật vậy ta có:
\(u_{k+1}=\dfrac{1}{2}u^2_k-u_k+2=\dfrac{1}{2}\left(u_k-2\right)^2+u_k\) (đúng)
Vậy un > 2 (n thuộc N*) (2)
Từ (1) (2) => un+1 - un > 0, hay un+1 > un
=> (un) là dãy tăng => \(\lim\limits_{n\rightarrow\infty}u_n=+\infty\)
2) \(2u_{n+1}=u^2_n-2u_n+4\)
\(\Leftrightarrow2u_{n+1}-4=u^2_n-2u_n\)
\(\Leftrightarrow2\left(u_{n+1}-2\right)=u_n\left(u_n-2\right)\)
\(\Leftrightarrow\dfrac{1}{u_{n+1}-2}=\dfrac{2}{u_n\left(u_n-2\right)}=\dfrac{1}{u_n-2}-\dfrac{1}{u_n}\)
\(\Leftrightarrow\dfrac{1}{u_n}=\dfrac{1}{u_n-2}-\dfrac{1}{u_{n+1}-2}\)
\(S=\dfrac{1}{u_1}+\dfrac{1}{u_2}+...+\dfrac{1}{u_n}\)
\(=\dfrac{1}{u_1-2}-\dfrac{1}{u_2-2}+\dfrac{1}{u_2-2}+...-\dfrac{1}{u_{n+1}-2}\)
\(=\dfrac{1}{u_1-2}-\dfrac{1}{u_{n+1}-2}\)
\(=2-\dfrac{1}{u_{n+1}-2}\)
\(\Leftrightarrow\lim\limits_{n\rightarrow\infty}S=2\)