Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét \(\Delta abe\)và \(\Delta hbe\)có:
\(\widehat{BAE}=\widehat{BHE}=90^O\)
BE LÀ CẠNH CHUNG
\(\widehat{ABE}=\widehat{HBE}\)(vì BE là đường phân giác của \(\widehat{B}\))
DO ĐÓ : T/G ABE = T/G HBE (G-C-G)

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

Ta có hình vẽ: B A C K F E H 1 2 1 2 1 2 1 2 I
a) Xét 2 \(\Delta\)vuông \(ABE\)và \(\Delta HBE\) có:
góc B1 = góc B2 (gt)
BE là cạnh huyền chung
=> \(\Delta ABE\) = \(\Delta HBE\) (cạnh huyền - góc nhọn)
b) Xét 2 \(\Delta\) \(ABI\)và \(\Delta HBI\) có:
góc B1 = góc B2 (gt)
AB = HB (vì \(\Delta ABE\) = \(\Delta HBE\))
AI là cạnh chung
=> \(\Delta ABI\)= \(\Delta HBI\) (c-g-c)
=> AI = HI (2 cạnh tương ứng)
=> góc I1 = góc I2 (2 góc tương ứng)
mà góc I1 + góc I2 = 180 độ
=> góc I1 = góc I2 = 180/2= 90 độ
=> BI \(\perp\) AH
=> BI là đường trung trực của đoạn thẳng AH
=> BE cũng là đường trung trực của đoạn thẳng AH (đpcm) (vì B, I , E nằm trên cùng 1 đoạn thẳng)
c)Xét \(\Delta\) vuông HEC có:
EC là cạnh đối diên với góc vuông (góc EHC)
=> EC là cạnh lớn nhất
=> EC > HE
mặt \(\ne\) HE = AE (vì\(\Delta ABE\) = \(\Delta HBE\))
=> EC > AE
d) Xét \(\Delta BKC\) có:
KH là đường cao thứ 1
CA là đường cao thứ 2
=> BF là đường cao thứ 3
=> BF \(\perp\) KC
=> BE \(\perp\) KC (đpcm) (vì B, E , F nằm trên cùng 1 đoạn thẳng)

MK cần bạn vẽ hình để giải được câu b và c nhé
Ta có AB vuông AC; EK vuông AC Nên AB song song với EK
=> goc BAE= goc AEK (1) ( hai góc so le trong)
Lại có góc BAE= góc BEA (2) ( do tam giác ABM= tam giác EBM chứng minh ở câu a)
(1)(2)=> góc AEB = góc AEK
c.
Xét \(\Delta AEH\)và \(\Delta AEK\)
\(H=K\)
Chung \(AE\)
\(\Rightarrow\Delta AEH=\Delta AEK\left(ch-gn\right)\Rightarrow\hept{\begin{cases}AH=AK\\HAE=KAE\end{cases}}\)
Gọi giao điểm giữa HK và AE là N
Xét \(\Delta AHN\)và \(\Delta AKN\)
\(AH=AK\left(cmt\right)\)
\(HAN=KAN\left(cmt\right)\)
Chung \(AN\)
\(\Rightarrow\Delta AHN=\Delta AKN\left(c.g.c\right)\Rightarrow AMH=AMK\Rightarrow2AMH=AMK+AMH=180\Rightarrow AMH=90\)
Vậy \(AE\perp HK\)tại \(N\)
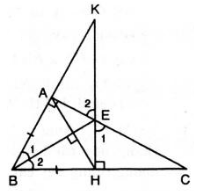


a) Xét hai tam giác vuông tam giác ABE và tam giác HBE ta có:
góc B1 = góc B2 (BE là phân giác của góc B)
BE: cạnh chung
=> tam giác ABE = tam giác HBE (cạnh huyền - góc nhọn)