Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABC}\) chung
Do đó; ΔAHB\(\sim\)ΔCAB
Suy ra: AB/CB=HB/AB
hay \(AB^2=HB\cdot BC\)
b: BC=25cm
BH=225:25=9(cm)
CH=25-9=16(cm)
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

mình tóm tắt thôi nha
▲MHA đồng dạng ▲HBA(g-g)
▲ABC đồng dạng ▲HBA(g-g)
suy ra ▲MHA đồng dạng ▲ABC
▲MHA đồng đăng ▲ANM
suy ra ▲ANM đồng dạng ▲ABC
suy ra tỉ số rồi ra
b)áp dụng PY-ta-go thì
BC =25cm
ta có S▲ABC =1/2 AB.AC
mặt khác S▲ABC=1/2 AH.BC
suy ra AB.AC=AH.BC
suy ra AH=(15.20)/25=12cm
ta có ▲ANM đồng dạng ▲ABC
suy ra \(\frac{NM}{BC}=\frac{AM}{AC}\)
\(\Rightarrow\frac{AH}{BC}=\frac{AM}{AC}=\frac{12}{25}\)
\(\Rightarrow\frac{S▲ANM}{S▲ABC}=\left(\frac{12}{25}\right)^2=0,2304\)
nhớ kick cho mình nha
câu b) tính tỉ số diện tích dùm mình lun nha bạn cần gắp lắm!!!!!!!!!!

a, Xét tam giác ABH và tam giác CBA ta có
^B _ chung
^AHB = ^BAC = 900
Vậy tam giác ABH ~ tam giác CBA (g.g)
\(\dfrac{AB}{BC}=\dfrac{BH}{AB}\Rightarrow AB^2=BH.BC\)(*)
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=25cm\)
Lại có (*) => \(BH=\dfrac{AB^2}{BC}=9cm\)
=> CH = BC - BH = 16 cm
c, Xét tam giác AHM và tam giác ABH có
^A _ chung
^AMH = ^AHB = 900
Vậy tam giác AHM ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AM}{AH}\Rightarrow AH^2=AM.AB\)(1)
Xét tam giác AHN và tam giác ACH có
^A _ chung
^ANH = ^AHC = 900
Vậy tam giác AHN ~ tam giác ACH (g.g)
\(\dfrac{AH}{AC}=\dfrac{AN}{AH}\Rightarrow AH^2=AN.AC\)(2)
Từ (1) ; (2) ta có AM . AB = AN . AC
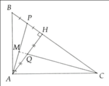
a. Xét ΔABC và ΔHBA có:
BAC=BHA=90o
B chung
⇒ ΔABC ∼ ΔHBA(g-g)
⇒ AB/BC=BH/AB
⇒ AB²=BC.BH
b. Xét ΔABC ⊥ A có: AH là đường cao
⇒ AB²+AC²=BC² (theo định lý Pitago)
⇒ BC²=15²+20²=225+400=625
⇒ BC=25 (cm)
Xét ΔABC ⊥ A có: AH là đường cao
⇒ AB²=BC.BH
⇔ BH=AB²/BC
⇔ BH=15²/25= 9(cm)
Ta có BH+HC=BC
⇒ HC=BC-BH
⇔ HC=25-9=16 (cm).
xin lỗi mk làm đc câu a à!!
Không sao cả, làm câu a) cũng được rồi á! Cảm ơn bạn nhiều nha!